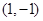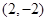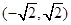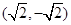题目内容
已知△PQR在直角坐标系中的位置如图所示：
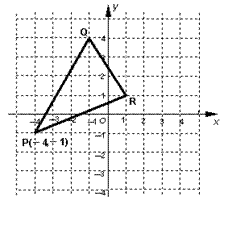
(1) 求出△PQR的面积；
(2) 画出△P′Q′R′，使△P′Q′R′与△PQR关于y轴对称，写出点P′、Q′、R′的坐标；
(3)连接PP′，QQ′，判断四边形QQ′P′P的形状，求出四边形QQ′P′P的面积．
(1) 求出△PQR的面积；
(2) 画出△P′Q′R′，使△P′Q′R′与△PQR关于y轴对称，写出点P′、Q′、R′的坐标；
(3)连接PP′，QQ′，判断四边形QQ′P′P的形状，求出四边形QQ′P′P的面积．
解：(1) S△PQR=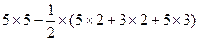
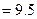
(2) △P′Q′R′就是所要画的三角形 各点坐标分别为P′(4,-1)、Q′(1,4)、
R′(-1,1)；(3)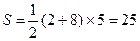
．
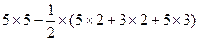
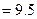
(2) △P′Q′R′就是所要画的三角形 各点坐标分别为P′(4,-1)、Q′(1,4)、
R′(-1,1)；(3)
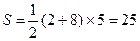．略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
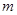, 1）在第二象限，则点B（
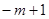，―1）必在第 象限；
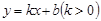和x轴上，已知点B1（1，1），B2（3，2），则B3的坐标是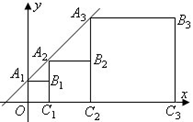 
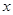轴上的点，点
，
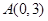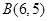则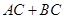
的最小值是（ ）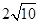
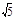，则该平行四边形的面积为 . 
