题目内容
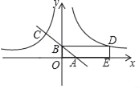
【题目】在平面直角坐标系中,⊙C的圆心坐标为(1,0),半径为1,![]() 为⊙C的直径,若点
为⊙C的直径,若点![]() 的坐标为(a,b)则点
的坐标为(a,b)则点![]() 的坐标为( )
的坐标为( )
A.(-a-1,-b)B.(-a+1,-b)C.(-a+2,-b)D.(-a-2,-b)
【答案】C
【解析】
作AD⊥x轴于D,BE⊥x轴于E,易证得△ACD≌△BCE,则AD=BE,DC=CE,由于点A的坐标为(a,b),⊙C的圆心坐标为(1,0),BE=AD=b,EC=CD=a-1,OE=1-(a-1)=-a+2,根据坐标的表示方法即可得到B点坐标为(-a+2,-b),同样得到当点A圆上的任何位置都有此结论.
解:如图,作AD⊥x轴于D,BE⊥x轴于E,
∵AB为⊙C的直径,∴CA=CB,
而∠ACD=∠BCE,
∴△ACD≌△BCE(AAS),
∴AD=BE,DC=CE,
∵点A的坐标为(a,b),⊙C的圆心坐标为(1,0),
∴BE=AD=b,EC=CD=a-1,
∴OE=1-(a-1)=-a+2,
∴B点坐标为(-a+2,-b),
当点A圆上的任何位置都有此结论.
故选:C.


练习册系列答案
相关题目