题目内容
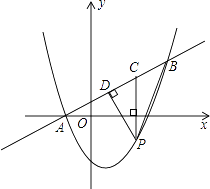
【题目】如图,抛物线y=﹣x2+bx+c与直线y= ![]() x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, ![]() ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.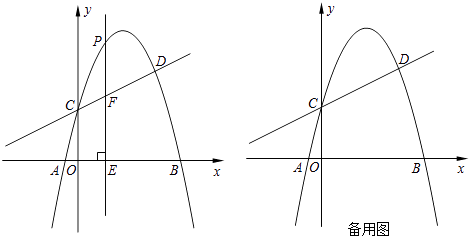
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
【答案】
(1)
解:在直线解析式y= ![]() x+2中,令x=0,得y=2,
x+2中,令x=0,得y=2,
∴C(0,2).
∵点C(0,2)、D(3, ![]() )在抛物线y=﹣x2+bx+c上,
)在抛物线y=﹣x2+bx+c上,
∴ 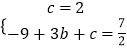 ,
,
解得b= ![]() ,c=2,
,c=2,
∴抛物线的解析式为:y=﹣x2+ ![]() x+2
x+2
(2)
解:∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=2,
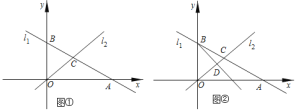
∴将直线y= ![]() x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
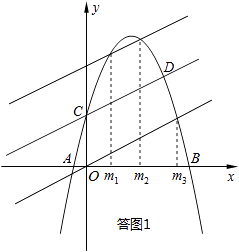
由答图1可以直观地看出,这样的交点有3个.
将直线y= ![]() x+2沿y轴向上平移2个单位,得到直线y=
x+2沿y轴向上平移2个单位,得到直线y= ![]() x+4,
x+4,
联立  ,
,
解得x1=1,x2=2,
∴m1=1,m2=2;
将直线y= ![]() x+2沿y轴向下平移2个单位,得到直线y=
x+2沿y轴向下平移2个单位,得到直线y= ![]() x,
x,
联立  ,
,
解得x3= ![]() ,x4=
,x4= ![]() (在y轴左侧,不合题意,舍去),
(在y轴左侧,不合题意,舍去),
∴m3= ![]() .
.
∴当m为值为1,2或 ![]() 时,以O、C、P、F为顶点的四边形是平行四边形
时,以O、C、P、F为顶点的四边形是平行四边形
(3)
解:存在.
理由:设点P的横坐标为m,则P(m,﹣m2+ ![]() m+2),F(m,
m+2),F(m, ![]() m+2).
m+2).
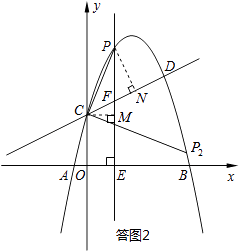
如答图2所示,过点C作CM⊥PE于点M,则CM=m,EM=2,
∴FM=yF﹣EM= ![]() m,
m,
∴tan∠CFM=2.
在Rt△CFM中,由勾股定理得:CF= ![]() m.
m.
过点P作PN⊥CD于点N,
则PN=FNtan∠PFN=FNtan∠CFM=2FN.
∵∠PCF=45°,
∴PN=CN,
而PN=2FN,
∴FN=CF= ![]() m,PN=2FN=
m,PN=2FN= ![]() m,
m,
在Rt△PFN中,由勾股定理得:PF= ![]() =
= ![]() m.
m.
∵PF=yP﹣yF=(﹣m2+ ![]() m+2)﹣(
m+2)﹣( ![]() m+2)=﹣m2+3m,
m+2)=﹣m2+3m,
∴﹣m2+3m= ![]() m,
m,
整理得:m2﹣ ![]() m=0,
m=0,
解得m=0(舍去)或m= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
同理求得,另一点为P( ![]() ,
, ![]() ).
).
∴符合条件的点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)首先求出点C的坐标,然后利用待定系数法求出抛物线的解析式;(2)本问采用数形结合的数学思想求解.将直线y= ![]() x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.
x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
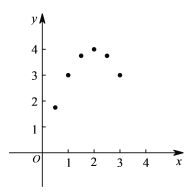
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.