题目内容
【题目】如图,在平面直角坐标系中,四边形 OABC 为菱形,点 C 的坐标为(4,0),∠AOC = 60°,垂直于 x 轴的直线 l 从 y 轴出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 l 与 菱形 OABC 的两边分别交与点 M、N(点 M 在点 N 的上方).
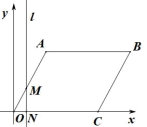
(1)求 A、B 两点的坐标;
(2)设 OMN 的面积为 S,直线 l 运动时间为 t 秒(0 ≤t ≤6 ),试求 S 与 t 的函数表达 式;
(3)在题(2)的条件下,t 为何值时,S 的面积最大?最大面积是多少.
【答案】(1)A(2,![]() ),B(6,
),B(6,![]() );(2)当
);(2)当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ;当
;当![]() 时,
时,![]() ;(3)
;(3)![]() 秒时,
秒时,![]() .
.
【解析】
(1)根菱形性质得出OA=AB=BC=CO=4,过A作AD⊥OC于D,求出AD、OD,即可得出答案;
(2)依题意可分为三种情况:①当0≤t≤2时,直线l与OA、OC两边相交,②当2<t≤4时,直线l与AB、OC两边相交,③当4<t≤6时,直线l与AB、BC两边相交,画出图形求出即可;
(3)根据(2)中各函数的性质和各自的自变量的取值范围可得出S的最大值及对应的t的值.
解:(1)∵四边形OABC为菱形,点C的坐标为(4,0),
∴![]()
过点A作![]() 于D.
于D.
∵![]()
∴![]() ,
,![]()
∴A(2,![]() ),B(6,
),B(6,![]() ).
).
(2)∵![]() ,
,
∴![]() ,
,
直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有三种情况:
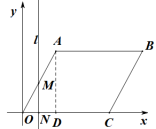
①当![]() 时,直线l与直线OA,OC两边相交,
时,直线l与直线OA,OC两边相交,
∴![]() ,
,
则![]() ;
;
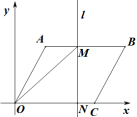
②当![]() 时,直线l与AB、OC两边相交,
时,直线l与AB、OC两边相交,
则![]() ;
;
③当![]() 时,直线l与AB、BC两边相交,
时,直线l与AB、BC两边相交,
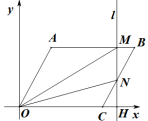
设直线l与x轴相交于H点,
∵![]() ,
,
∴![]() ;
;
综上所述: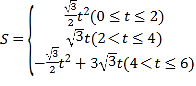 ,
,
(3)由(2)知,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
∵![]() 的对称轴为
的对称轴为![]() ,
,
∴函数![]() ,当
,当![]() 时,S随
时,S随![]() 的增大而减小,
的增大而减小,
即![]() 时,S取得最大值:
时,S取得最大值:![]() ,
,
综上所述,当![]() 秒时,
秒时,![]() .
.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸(![]() ),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
尺寸 | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 |
| 9.03 | 9.04 | 9.06 | 9.07 | 9.08 |
|
按照生产标准,产品等级规定如下:
尺寸(单位: | 产品等次 |
| 特等品 |
| 优等品 |
| 合格品 |
| 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格个数时,将优等品(含特等品)算在内,
(1)已知此次抽检的合格率为![]() ,请判断编号为15的产品是否为合格品,并说明理由;
,请判断编号为15的产品是否为合格品,并说明理由;
(2)已知此次及抽检出的优等品尺寸的中位数为![]() .
.
①![]() __________;
__________;
②将这些优等品分成两组,一组尺寸大于![]() ,另一种尺寸不大于
,另一种尺寸不大于![]() ,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.