Question

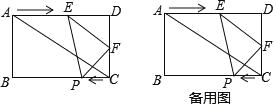
【题目】如图，在矩形 ABCD 中，AB＝6cm，AD＝8cm，直线 EF 从点 A 出发沿 AD 方向匀速运动，速度是 2cm/s，运动过程中始终保持 EF∥AC．F 交

AD 于 E，交 DC 于点 F；同时，点 P 从点 C 出发沿 CB 方向匀速运动，速度是 1cm/s，连接 PE、PF，设运动时间 t（s）（0＜t＜4）．

（1）当 t＝1 时，求 EF 长；

（2）求 t 为何值时，四边形 EPCD 为矩形；

（3）设△PEF 的面积为 S（cm2），求出面积 S 关于时间 t 的表达式；

（4）在运动过程中，是否存在某一时刻使 S△PC F：S 矩形 ABCD＝3：16？若存在， 求出 t 的值；若不存在，请说明理由．

Answer 1

【答案】（1）EF＝；（2）当 t＝ 时，四边形 EPCD 为矩形；（3）S＝﹣t2+9t（0＜t＜4）；（4）存在，当 t＝2 时，S△PCF：S 矩形 ABCD＝3：16．

【解析】

（1）由勾股定理知AC=10，由题意得AE=2，DE=6，根据EF∥AC知△DEF∽△DAC，据此得代入计算;

（2）由DE∥CP且∠D=∠C知DE=CP时，四边形EPCD为矩形，据此求解

（3）证△DEF∽△DAC得,据此求得,根据S=S梯形DEPC-S△DEF-S△PCF可得函数解析式；

（4）由S矩形ABCD=AB×AD=48，且S△PCF：S矩形ABCD=3：16知S△PCF=9，再根据可得关于t的方程，解之可得．

解：（1）∵AB＝6cm，AD＝8cm，

∴AC＝10cm，

当 t＝1 时，AE＝2， 则 DE＝6，

∵EF∥AC，

∴△DEF∽△DAC，

∴，即

解得：

（2）由题意知 AE＝2t，CP＝t， 则 DE＝8﹣2t，

∵四边形 EPCD 是矩形，

∴DE＝CP，即 8﹣2t＝t， 解得 t＝ ，

故当 t＝时，四边形 EPCD 为矩形；

（3）∵EF∥AC，

∴△DEF∽△DAC，

，即

解得：

则 CF＝CDDF＝6﹣（6﹣t）＝t，

则 S＝S 梯形 DEPC﹣S△DEF﹣S△PCF

＝×（8﹣2t+t）×6﹣ ×（8﹣2t）×（6﹣t）﹣×t×t

＝﹣t2+9t，

即 S＝﹣t2+9t（0＜t＜4）；

（4）存在，

∵S 矩形 ABCD＝AB×AD＝48，且 S△PCF：S 矩形 ABCD＝3：16，

∴S△PCF＝9，

又∵S△PCF＝×t×t＝t2，

∴t2＝9，

解得：t＝2或 t＝﹣2（舍），

∴当 t＝2时，S△PCF：S 矩形 ABCD＝3：16．