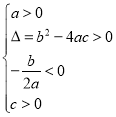题目内容
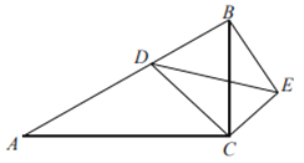
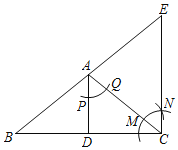
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() , 且OC=4,求PB的长.
, 且OC=4,求PB的长.
【答案】(1)证明见解析(2)PB=3![]()
【解析】
(1)通过证明△PAO≌△PBO可得结论;
(2)根据tan∠BAD=![]() ,且OC=4,可求出AC=6,再证得△PAC∽△AOC,最后利用相似三角形的性质以及勾股定理求得答案.
,且OC=4,可求出AC=6,再证得△PAC∽△AOC,最后利用相似三角形的性质以及勾股定理求得答案.
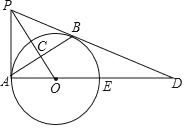
解:(1)连结OB,则OA=OB,如图1,
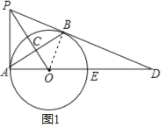
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵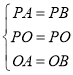 ,
,
∴△PAO≌△PBO(SSS),
∴∠PBO=∠PAO,
∵PB为⊙O的切线,B为切点,
∴PB⊥OB,
∴∠PBO=90°,
∴∠PAO=90°,即PA⊥OA,
∴PA是⊙O的切线;
(2)∵在Rt△AOC中,tan∠BAD=tan∠CAO=![]() ,且OC=4,
,且OC=4,
∴AC=6,则BC=6,
∴![]() ,
,
在Rt△APO中,AC⊥OP,
易得△PAC∽△AOC,
∴![]() ,即AC2=OCPC,
,即AC2=OCPC,
∴PC=9,
∴OP=PC+OC=13,
在Rt△PBC中,由勾股定理,得PB=![]() .
.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
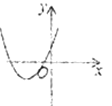
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.