题目内容
 如图,已知等腰三角形ABC中,底边BC=24cm,△ABC的面积等于60cm2.
如图,已知等腰三角形ABC中,底边BC=24cm,△ABC的面积等于60cm2.(1)求腰AB的长;
(2)若D、E分别是AB、AC的中点,求DE的长.
分析:(1)作AD⊥BC于D.根据三角形的面积公式求得AD的长,结合等腰三角形的三线合一的性质和勾股定理即可求得腰长.
(2)直接利用三角形的中位线定理得到结论即可.
(2)直接利用三角形的中位线定理得到结论即可.
解答: 解:(1)作AD⊥BC于D.
解:(1)作AD⊥BC于D.
则S△ABC=
AD•BC=60,
∵BC=24,
∴AD=5,
在Rt△ABD中,AB=
=
=13cm.
(2)∵D、E分别是AB、AC的中点,
∴DE是三角形ABC的中位线
∴DE=
BC=
×24=12cm.
 解:(1)作AD⊥BC于D.
解:(1)作AD⊥BC于D.则S△ABC=
| 1 |
| 2 |
∵BC=24,
∴AD=5,
在Rt△ABD中,AB=
| AD2+BD2 |
| 52+122 |
(2)∵D、E分别是AB、AC的中点,
∴DE是三角形ABC的中位线
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等腰三角形的性质、勾股定理及三角形的中位线定理,解题的关键是作出BC边上的高并正确的利用等腰三角形的三线合一的性质.

练习册系列答案
相关题目
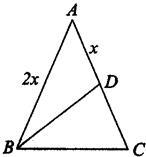 22、如图,已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分,求它的底边BC的长.
22、如图,已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分,求它的底边BC的长. 如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.
如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.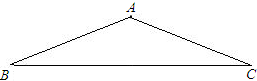
 15、如图,已知等腰三角形ABC中,AC=BC,D为BC边上一点,且AB=AD,若不再添加辅助线,图中与∠C相等的角是
15、如图,已知等腰三角形ABC中,AC=BC,D为BC边上一点,且AB=AD,若不再添加辅助线,图中与∠C相等的角是 如图,已知等腰三角形ABC,顶点A的坐标是(
如图,已知等腰三角形ABC,顶点A的坐标是(