题目内容
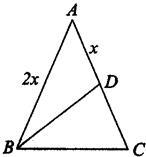22、如图，已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分，求它的底边BC的长．分析：分两种情况讨论：当AB+AD=12，BC+DC=15或AB+AD=15，BC+DC=12，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为8，8，11或10，10，7．所以BC的长为7cm或11cm．
解答：解：设AD=x则，当2x+x=12时，x=4，即AB=AC=8，
∵周长是12+15=27，∴BC=11cm；
当2x+x=15时，x=5，即AB=AC=10，
∵周长是12+15=27，∴BC=7cm，
综上可知，底边BC的长为7cm或11cm．
∵周长是12+15=27，∴BC=11cm；
当2x+x=15时，x=5，即AB=AC=10，
∵周长是12+15=27，∴BC=7cm，
综上可知，底边BC的长为7cm或11cm．
点评：主要考查了等腰三角形的性质．解题的关键是利用等腰三角形的两腰相等和中线的性质求出腰长，再利用周长的概念求得边长．
练习册系列答案
相关题目
如图，已知等腰三角形ADC，AD=AC，B是线段DC上的一点，连接AB，且有AB=DB．
15、如图，已知等腰三角形ABC中，AC=BC，D为BC边上一点，且AB=AD，若不再添加辅助线，图中与∠C相等的角是
如图，已知等腰三角形ABC，顶点A的坐标是（