题目内容
如图，已知等腰三角形ADC，AD=AC，B是线段DC上的一点，连接AB，且有AB=DB．（1）△ABD∽△DAC；
（2）若△ABC的周长是15，且
| AB |
| AC |
| 2 |
| 3 |
分析：（1）由AD=AC，∠D=∠C，AB=DB，∠D=∠DAB．∠DAB=∠D=∠C．利用对应角相等可证明△DAB∽△DCA．
（2）由（1）得
=
=
．和△ABC的周长是15，即可解题．
（2）由（1）得
| AD |
| DC |
| AB |
| AC |
| 2 |
| 3 |
解答：（1）证明：∵AD=AC，
∴∠D=∠C．
又∵AB=DB，
∴∠D=∠DAB．∴∠DAB=∠D=∠C．
又∵∠D=∠D，
∴△DAB∽△DCA．
（2）解：由（1）得
=
=
．
∴3AD=2DC．
即3AC=2DC．
∵△ABC的周长是15厘米，
即AB+BC+AC=15，
则有DB+BC+AC=15．
∴DC+AC=15．
∴AC=6．
∴∠D=∠C．
又∵AB=DB，
∴∠D=∠DAB．∴∠DAB=∠D=∠C．
又∵∠D=∠D，
∴△DAB∽△DCA．
（2）解：由（1）得
| AD |
| DC |
| AB |
| AC |
| 2 |
| 3 |
∴3AD=2DC．
即3AC=2DC．
∵△ABC的周长是15厘米，
即AB+BC+AC=15，
则有DB+BC+AC=15．
∴DC+AC=15．
∴AC=6．
点评：此题考查学生利用等腰三角形的性质和两角对应相等来判定相似三角形，再用相似三角形对应边成比例的特点来求得三角形的边长，总之，此题难度不大，是一道基础题．
练习册系列答案
相关题目
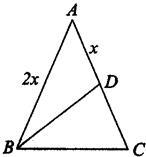22、如图，已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分，求它的底边BC的长．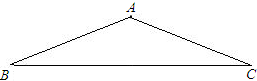
15、如图，已知等腰三角形ABC中，AC=BC，D为BC边上一点，且AB=AD，若不再添加辅助线，图中与∠C相等的角是
如图，已知等腰三角形ABC，顶点A的坐标是（