题目内容
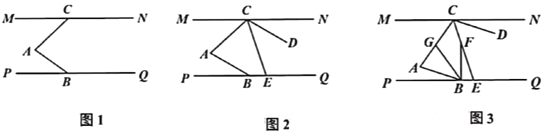
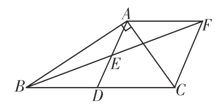
【题目】如图1,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB点E,DF⊥BC于点F.将∠EDF绕点D顺时针旋转α°(0<α<180),其两边的对应边DE′、DF′分别与直线AB、BC相交于点G、P,如图2.连接GP,当△DGP的面积等于3![]() 时,则α的大小为( )
时,则α的大小为( )
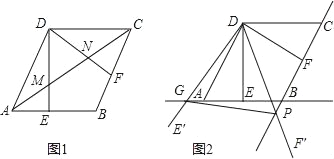
A. 30 B. 45 C. 60 D. 120
【答案】C
【解析】分析题目根据AB∥DC,∠BAD=60°,可得∠ADC的度数;
利用∠ADE=∠CDF=30°,可得∠EDF的度数,当∠EDF顺时针旋转时,由旋转的性质可知:∠EDG=∠FDP,∠GDP=∠EDF=60°,根据全等三角形的判定方法证明△DEG≌△DFP;
然后全等三角形的性质可得DG=DP,即可得出△DGP为等边三角形,利用面积和cos∠EDG可得∠EDG的度数,同理可得结论.
∵AB∥DC,∠BAD=60°,
∴∠ADC=120°,又∠ADE=∠CDF=30°,
∴∠EDF=60°,
由旋转的性质可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,
DE=DF=![]() ,∠DEG=∠DFP=90°,
,∠DEG=∠DFP=90°,
在△DEG和△DFP中,
![]() ,
,
∴△DEG≌△DFP,
∴DG=DP,
∴△DGP为等边三角形,
∴△DGP的面积=![]() DG2=3
DG2=3![]() ,
,
解得,DG=2![]() ,
,
则cos∠EDG=![]() =
=![]() ,
,
∴∠EDG=60°,
∴当顺时针旋转60°时,△DGP的面积等于3![]() ,
,
故选:C.

 名校课堂系列答案
名校课堂系列答案【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
![]()
成绩段 | 频数 | 频率 |
0≤x<20 | 5 | 0.1 |
20≤x<40 | 10 | a |
40≤x<60 | b | 0.14 |
60≤x<80 | m | c |
80≤x<100 | 12 | n |
![]()
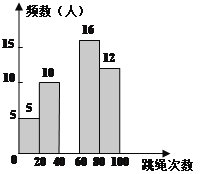
根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多人?
【题目】2019年小张前五个月的奖金变化情况如下表(正数表示比前一月多的钱数,负数表示比前一月少的钱数,单位:元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 |
钱数变化 |
|
|
|
|
|
若2018年12月份小张的奖金为![]() 元.
元.
(1)用代数式表示2019年二月份小张的奖金为___________元;
(2)小张五月份所得奖金比二月份多多少?