题目内容
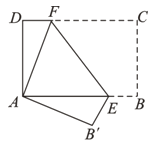
【题目】如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕EF分别与AB、DC交于点E和点F， 点B的对应点为B′．
（1）证明：AE=CF；
（2）若AD＝12，DC＝18，求DF的长．
【答案】（1）见解析；（2）5.
【解析】
（1）根据折叠的性质以及矩形的性质，运用ASA即可判定△ADF≌△AB′E；
（2）先设FA=FC=x，则DF=DC-FC=18-x，根据Rt△ADF中，AD2+DF2=AF2，即可得出方程122+（18-x）2=x2，解得x=13．所在DF=18-13=5.
（1）证明：∵四边形ABCD是矩形，
∴∠D=∠C=∠B′=90°，AD=CB=AB′，
∵∠DAF+∠EAF=90°，∠B′AE+∠EAF=90°，
∴∠DAF=∠B′AE，
在△ADF和△AB′E中，
，
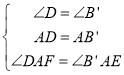∴△ADF≌△AB′E（ASA）．
∴AE=CF；
（2）解：由折叠性质得FA=FC，
设FA=FC=x，则DF=DC-FC=18-x，
在Rt△ADF中，AD2+DF2=AF2，
∴122+（18-x）2=x2．
解得x=13．
∴DF=18-13=5
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：g） |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
这批样品的平均质量比标准质量多还是少？多或少几克？若每袋标准质量为500克，则抽样检测的总质量是多少？
