题目内容
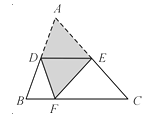
【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
A. 6![]() B. 7
B. 7![]() C. 8
C. 8![]() D. 9
D. 9![]()
【答案】C
【解析】先解直角△ABC,得出BC=AB×cosB=18×![]() =12,AC=
=12,AC=![]() =6
=6![]() . 再根据旋转的性质得出BC=DC=6,AC=EC=3
. 再根据旋转的性质得出BC=DC=6,AC=EC=3![]() ,∠BCD=∠ACE,利用等边对等角以及三角形内角和定理得出∠B=∠CAE,作CM⊥BD于M,作CN⊥AE于N,则∠BCM=
,∠BCD=∠ACE,利用等边对等角以及三角形内角和定理得出∠B=∠CAE,作CM⊥BD于M,作CN⊥AE于N,则∠BCM=![]() ∠BCD,∠ACN=
∠BCD,∠ACN=![]() ∠ACE,∠BCM=∠ACN,解直角△ANC求出AN=AC×cos∠CAN=6
∠ACE,∠BCM=∠ACN,解直角△ANC求出AN=AC×cos∠CAN=6![]() ×
×![]() =4
=4![]() ,根据等腰三角形三线合一的性质得出AE=2AN=8
,根据等腰三角形三线合一的性质得出AE=2AN=8![]() .
.
解:∵在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,
,
∴BC=AB×cosB=18×![]() =12,AC=
=12,AC=![]() =6
=6![]() .
.
∵把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,
∴△ABC≌△EDC,BC=CD=12,AC=EC=6![]() ,∠BCD=∠ACE,
,∠BCD=∠ACE,
∴∠B=∠CAE.
作CN⊥AE于N,则∠BCM=![]() ∠BCD,∠ACN=
∠BCD,∠ACN=![]() ∠ACE,
∠ACE,
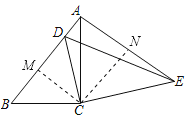
∴∠BCM=∠ACN,
∵在△ANC中,∠ANC=90°,AC=6![]() ,cos∠CAN=cosB=
,cos∠CAN=cosB=![]() ,
,
∴AN=AC×cos∠CAN=6![]() ×
×![]() =4
=4![]() ,
,
∴AE=2AN=8![]() .
.
故答案为:8![]() .
.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目