题目内容
如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.

(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.

(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
解:(1)菱形。理由如下:
∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形。
(2)连接EF,

∵AE=AF,∠A=60°,∴△EAF是等边三角形。
∴EF=AE=8厘米。
∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形。
(2)连接EF,

∵AE=AF,∠A=60°,∴△EAF是等边三角形。
∴EF=AE=8厘米。
试题分析:(1)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形。
(2)首先连接EF,由AE=AF,∠A=60°,可证得△EAF是等边三角形,则可求得线段EF的长。

练习册系列答案
相关题目
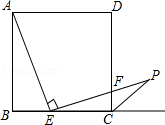
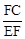 的值为 ;
的值为 ; ADCE中,DE最小的值是
ADCE中,DE最小的值是