题目内容
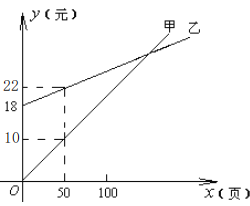
【题目】已知直线 y13x 6与 x 轴、y 轴分别交于点 A,C;过点 C 的直线 y2x b 与 x 轴交于点 B.
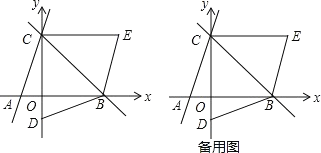
(1)b 的值为 ;
(2)若点 D 的坐标为(0,﹣2),将△BCD 沿直线 BC 对折后,点 D 落到第一象限的点 E 处, 求证:四边形 ABEC 是平行四边形;
(3)在直线 BC 上是否存在点 P,使得以 P、A、D、B 为顶点的四边形是平行四边形? 如果存在,请求出点 P 的坐标;如果不存在,请说明理由.
【答案】(1) 6; (2)见解析; (3)存在,点P的坐标为(4,2)或(8,![]() )
)
【解析】
(1)先由点C在直线![]() 上,求出点C坐标,代入直线
上,求出点C坐标,代入直线![]() 中即可;
中即可;
(2)先求出∠OBC=∠OCB=45°,进而判断出CE∥AB,最后判断出CE=AB即可;
(3) ∠OAD=∠ODA=45![]() ,∠OBC=∠OCB=45°,判断出AD∥BC,使得以P、A、D、B为顶点的四边形是平行四边形,只要AD=PB即可,利用两点之间的距离公式即可得出点P坐标.
,∠OBC=∠OCB=45°,判断出AD∥BC,使得以P、A、D、B为顶点的四边形是平行四边形,只要AD=PB即可,利用两点之间的距离公式即可得出点P坐标.
(1)∵直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点C,
轴交于点C,
令![]() ,则
,则![]() ,
,
∴点C的坐标为(0,6),
∵直线![]() 过点C,
过点C,
将点C的坐标为(0,6)代入![]() ,
,
解得:![]() ,
,
故答案为:6;
(2)当![]() 时,直线BC的解析式为
时,直线BC的解析式为![]() ,
,
∵点C的坐标为(0,6),
∴OC=6,
令![]() 得,
得,![]() ,
,
∴点B的坐标为(6,0),
∴OB=6,
∴OB=OC=6,
∴∠OBC=∠OCB=45°,
由折叠的性质得:∠BCE=∠OCB=45°,CE=CD,
∴∠OBC=∠BCE=45![]() ,
,
∴CE∥AB,
由![]() ,令
,令![]() 得,
得,![]() ,
,
∴点A的坐标为(![]() ,0),
,0),
∴OA=2,
∴AB=OA+OB=2+6=8,
∵点D的坐标为(0,![]() ),
),
∴OD=2,
∴CE=CD=OC+OD=8,
∴CE=AB,
又∵CE∥AB,
∴四边形ABEC为平行四边形;
(3)存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
如图,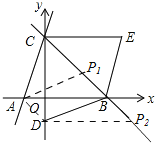
∵点A的坐标为(![]() ,0)、点D的坐标为(0,
,0)、点D的坐标为(0,![]() ),
),
∴OA=OD=2,
∴![]() ,∠OAD=∠ODA=45
,∠OAD=∠ODA=45![]() ,
,
由(2)得:∠OBC=∠BCE=45![]() ,
,
∴∠OBC=∠BCE=∠OAD=∠ODA=45![]() ,
,
∴AD∥BC,
∵直线BC解析式为![]() ,且点P在直线BC上,
,且点P在直线BC上,
∴设点P坐标为(![]() ,
,![]() ),
),
∴![]()
![]()
![]() ,
,
∵以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴P(4,2)或P(8,![]() ),
),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
点P的坐标为(4,2)或(8,![]() ).
).

【题目】现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
占地面积(m/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 30 | 160 | 1.1 |
草莓 | 15 | 50 | 1.6 |
(1)若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?