题目内容
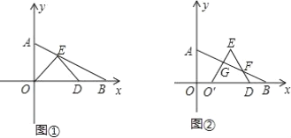
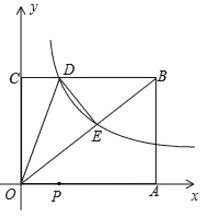
【题目】如图,已知矩形![]() 的两边OA,OC分别落在
的两边OA,OC分别落在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() 的中点E,且与BC边相交于点D.
的中点E,且与BC边相交于点D.
(1)①求反比例函数的解析式及点D的坐标;
②直接写出![]() 的面积为________.
的面积为________.
(2)若P是OA上的动点,当![]() 值为最小时,求直线
值为最小时,求直线![]() 的解析式.
的解析式.
【答案】(1)①反比例函数的解析式为![]() ;点D坐标为
;点D坐标为![]() ;②
;②![]() ;(2)直线PE的解析式为
;(2)直线PE的解析式为![]() .
.
【解析】
(1)①由E是OB的中点,即可求得E的坐标,利用待定系数法求得函数的解析式,进而求得D的坐标;
②根据S△ODE=S△OBC-S△OCD-S△BDE即可求解;
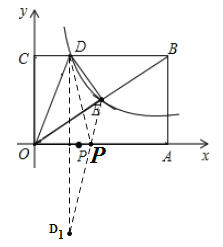
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,
,![]() 与
与![]() 轴的交点P即为所求.利用待定系数法即可求出解析式.
轴的交点P即为所求.利用待定系数法即可求出解析式.
(1)①∵E是OB的中点,顶点B的坐标是![]() ,
,
∴E点坐标为![]() .
.
将点![]() 代入
代入![]() 中,得
中,得![]() .
.
∴反比例函数的解析式为![]() .
.
令![]() ,则
,则![]() ,
,
∴点D坐标为![]() .
.
②S△OBC=![]() BCOC=
BCOC=![]() ×6×4=12,
×6×4=12,
S△OCD=![]() OCCD=
OCCD=![]() ×4×img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/02/023f94ae/SYS202007220205239681262012_DA/SYS202007220205239681262012_DA.017.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:page; -aw-rel-vpos:page; -aw-top-pos:0pt; -aw-wrap-type:inline" />=3,
×4×img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/02/023f94ae/SYS202007220205239681262012_DA/SYS202007220205239681262012_DA.017.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:page; -aw-rel-vpos:page; -aw-top-pos:0pt; -aw-wrap-type:inline" />=3,
S△BDE=![]() ×(
×(![]() )×2=
)×2=![]() ,
,
则S△ODE=S△OBC-S△OCD-S△BDE=12-3-3-4.5=![]() .
.
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() .
.
连接![]() ,
,![]() 与
与![]() 轴的交点P即为所求.
轴的交点P即为所求.
设直线PE解析式为![]() ,依题意得
,依题意得
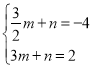 ,解得
,解得![]()
∴直线PE的解析式为![]() .
.

【题目】某微商销售的某商品每袋成本20元,设销售价格为x(单位:元/袋),该微商发现销售量y与销售价格x之间的关系如表:
销售价格x(元/袋) | 25 | 30 | 35 | 40 |
销售件数y | 275 | 250 | 225 | 200 |
(1)求y关于x的函数表达式;
(2)根据物价部门的规定,商品的利润率不能超过100%,该微商应该如何定价,才能使获得的利润最大,最大利润是多少?