题目内容
【题目】长方形ABCD中,AB=6,AD=8,点E为边AD上一点,将△ABE沿BE折叠后得到△BEF.

(1)如图1,若点E为AD的中点,延长BF交边CD于点G.
①求证:DG=FG.
②求FG的长度.
(2)如图2,若点E为边AD的一动点,连接FD,△DEF能否为直角三角形?若能,求出AE的值.若不能,请说明理由.
【答案】(1)①见解析;②![]() ;(2)3或6
;(2)3或6
【解析】
(1) ①连接EG,证明Rt△EGD≌Rt△EGF,即可解决问题;
②设DG=GF=x则GC=6-x,在Rt△BCG中利用勾股定理求解;
(2)需要分类讨论:当∠EFD=90°时,B,F,D共线,设AE=EF=x;
当∠FED=90°时,AE=AB=6.
解:(1)①证明:如图1中,连接EG,
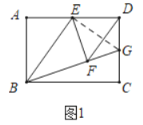
∵四边形ABCD是矩形,
∴∠A=∠EDG=90°,
∵EA=EF=ED,∠A=∠EFB=90°,
∴∠EFG=∠EDG=90°,
∵EG=EG,EF=ED,
∴Rt△EGD≌Rt△EGF(HL),
∴GD=GF.
②解:如图1中,设DG=GF=x则GC=6-x,
在Rt△BCG中,∵![]() =
=![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
∴GF=![]() .
.
(2)解:存在.如图2中,当∠EFD=90°时,B,F,D共线,设AE=EF=x,
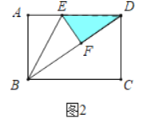
在Rt△ABD中,BD=10,
∵BF=BA=6,
∴DF=10-6=4
在Rt△EFD中,∵![]() ,
,
∴![]() ,
,
∴x=3,
∴AE=3.
如图3中,当∠FED=90°时,AE=AB=6.
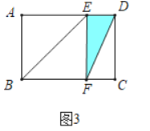
综上所述,满足条件的AE的值为3或6.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目