题目内容
若(3x+1)4=ax4+bx3+cx2+dx+e,则a﹣b+c﹣d+e= .
16
试题分析:先利用完全平方公式计算一次,再用多项式乘以多项式计算,结果合并后等于ax4+bx3+cx2+dx+e,利用等式对应相等的性质,可求a、b、c、d、e,代入所求式子求值即可.
解:∵(3x+1)4=(9x2+6x+1)2=81x4+108x3+54x2+12x+1,
(3x+1)4=ax4+bx3+cx2+dx+e,
∴81x4+108x3+54x2+12x+1=ax4+bx3+cx2+dx+e,
∴a=81,b=108,c=54,d=12,e=1,
∴a﹣b+c﹣d+e=81﹣108+54﹣12+1=16.
故答案是16.
点评:本题主要考查多项式乘以多项式的法则、完全平方公式以及等式的对应相等的性质.

练习册系列答案
相关题目
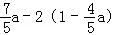 的值为 _____ .
的值为 _____ .