题目内容
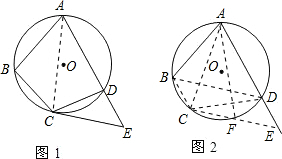
如图（1），四边形ABCD是⊙O的内接四边形，点C是
的中点，过点C的切线与AD的延长线交于点E．
（1）求证：AB•DE=CD•BC；
（2）如果四边形ABCD仍是⊙O的内接四边形，点C在劣弧
上运动，点E在AD的延长线上运动，切线CE变为割线EFC，请问要使（1）的结论
成立还需要具备什么条件？请你在图（2）上画出示意图，标明有关字母，不要求进行证明．
 |
| BD |
（1）求证：AB•DE=CD•BC；
（2）如果四边形ABCD仍是⊙O的内接四边形，点C在劣弧
|
| BD |
成立还需要具备什么条件？请你在图（2）上画出示意图，标明有关字母，不要求进行证明．（1）证明：连接AC．
∵C是
的中点，
∴
=
，∠BAC=∠DAC
∵CE切⊙O于点C，点C在⊙O上
∴∠DCE=∠DAC=∠BAC，
∵四边形ABCD是⊙O的内接四边形，
∴∠EDC=∠B，
∴△EDC∽△CBA，
∴
=
，
∴AB•DE=CD•BC；
（2）如图，条件为：
=
（或DF=BC或∠DAF=∠BAC
或∠DCF=∠BAC或FC∥BD等）
如图，（图中虚线为可能画的线）．
∵C是
|
| BD |
∴
|
| BC |
|
| DC |
∵CE切⊙O于点C，点C在⊙O上
∴∠DCE=∠DAC=∠BAC，
∵四边形ABCD是⊙O的内接四边形，
∴∠EDC=∠B，
∴△EDC∽△CBA，
∴
| AB |
| CD |
| BC |
| DE |
∴AB•DE=CD•BC；
（2）如图，条件为：
|
| DF |
|
| BC |
或∠DCF=∠BAC或FC∥BD等）
如图，（图中虚线为可能画的线）．
练习册系列答案
相关题目
