̀âÄ¿ÄÚÈƯ
¡¾̀âÄ¿¡¿Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬![]()
![]() £¬²¢Ç̉
£¬²¢Ç̉![]() Âú×ă
Âú×ă![]() .̉»¶¯µă
.̉»¶¯µă![]() ´Óµă
´Óµă![]() ³ö·¢£¬ÔÚÏ߶Î
³ö·¢£¬ÔÚÏ߶Î![]() ÉÏ̉ÔĂ¿Ăë
ÉÏ̉ÔĂ¿Ăë![]() ¸öµ¥Î»³¤¶ÈµÄËÙ¶ÈỊ̈µă
¸öµ¥Î»³¤¶ÈµÄËÙ¶ÈỊ̈µă![]() ̉ƶ¯£»¶¯µă
̉ƶ¯£»¶¯µă![]() ´Óµă
´Óµă![]() ³ö·¢ÔÚÏ߶Î
³ö·¢ÔÚÏ߶Î![]() ÉÏ̉ÔĂ¿Ăë
ÉÏ̉ÔĂ¿Ăë![]() ¸öµ¥Î»³¤¶ÈµÄËÙ¶ÈỊ̈µă
¸öµ¥Î»³¤¶ÈµÄËÙ¶ÈỊ̈µă![]() Ô˶¯£¬µă
Ô˶¯£¬µă![]() ·Ö±đ´Óµă
·Ö±đ´Óµă![]() ͬʱ³ö·¢£¬µ±µă
ͬʱ³ö·¢£¬µ±µă![]() Ô˶¯µ½µă
Ô˶¯µ½µă![]() ʱ£¬µă
ʱ£¬µă![]() Ëæֹ֮ͣÔ˶¯.ÉèÔ˶¯Ê±¼äΪ
Ëæֹ֮ͣÔ˶¯.ÉèÔ˶¯Ê±¼äΪ![]() (Ăë)
(Ăë)

(1)Çó![]() Á½µăµÄ×ø±ê£»
Á½µăµÄ×ø±ê£»
(2)µ±![]() ΪºÎֵʱ£¬ËıßĐÎ
ΪºÎֵʱ£¬ËıßĐÎ![]() ÊÇƽĐĐËıßĐΣ¿²¢Çó³ö´Ëʱ
ÊÇƽĐĐËıßĐΣ¿²¢Çó³ö´Ëʱ![]() Á½µăµÄ×ø±ê.
Á½µăµÄ×ø±ê.
(3)µ±![]() ΪºÎֵʱ£¬
ΪºÎֵʱ£¬![]() ÊÇ̉Ô
ÊÇ̉Ô![]() ΪÑüµÄµÈÑüÈư½ÇĐΣ¿²¢Çó³ö´Ëʱ
ΪÑüµÄµÈÑüÈư½ÇĐΣ¿²¢Çó³ö´Ëʱ![]() Á½µăµÄ×ø±ê.
Á½µăµÄ×ø±ê.
¡¾´đ°¸¡¿(1)![]() £»(2)
£»(2)![]() £»(3)
£»(3) ![]() »̣
»̣![]() .
.
¡¾½âÎö¡¿
(1)Óɶ₫´Î¸ùʽÓĐ̉ẩåµÄ̀ơ¼₫¿ÉÇó³öa¡¢bµÄÖµ£¬ÔÙ¸ù¾ỬÑÖª¼´¿ÉÇóµĂ´đ°¸£»
(2)ÓÉ̀ẩâµĂ£º![]() £¬Ộ
£¬Ộ![]() £¬µ±
£¬µ±![]() ʱ£¬ËıßĐÎ
ʱ£¬ËıßĐÎ![]() ÊÇƽĐĐËıßĐΣ¬ÓÉ´Ë¿ÉµĂ¹ØÓÚtµÄ·½³̀£¬Çó³ötµÄÖµ¼´¿ÉÇóµĂ´đ°¸£»
ÊÇƽĐĐËıßĐΣ¬ÓÉ´Ë¿ÉµĂ¹ØÓÚtµÄ·½³̀£¬Çó³ötµÄÖµ¼´¿ÉÇóµĂ´đ°¸£»
(3)·Ö![]() ¡¢
¡¢![]() Á½ÖÖÇé¿ö·Ö±đ»³ö·ûºÏ̀ẩâµÄͼĐΣ¬
Á½ÖÖÇé¿ö·Ö±đ»³ö·ûºÏ̀ẩâµÄͼĐΣ¬
(1)ÓÉ![]() £¬
£¬
Ộ![]() £¬
£¬
![]() £¬
£¬
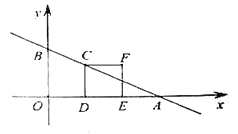
¡ßAB//OC£¬A(0£¬12)£¬B(a£¬c)£¬
¡àc=12£¬
¡à![]() £»
£»
(2)Èçͼ£¬
ÓÉ̀ẩâµĂ£º![]() £¬
£¬
Ộ£º![]() £¬
£¬
![]() µ±
µ±![]() ʱ£¬ËıßĐÎ
ʱ£¬ËıßĐÎ![]() ÊÇƽĐĐËıßĐΣ¬
ÊÇƽĐĐËıßĐΣ¬
![]() £¬
£¬
½âµĂ£º![]() £¬
£¬
![]() £»
£»
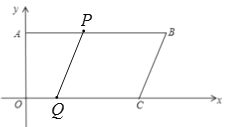
(3)µ±![]() ʱ£¬¹ư
ʱ£¬¹ư![]() ×÷
×÷![]() £¬ỘËıßĐÎAOQNÊǾØĐΣ¬
£¬ỘËıßĐÎAOQNÊǾØĐΣ¬
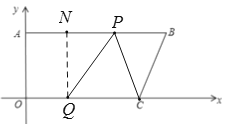
¡àAN=OQ=t£¬QN=OA=12£¬
¡àPN=t£¬
ÓÉ̀ẩâµĂ£º![]() £¬
£¬
½âµĂ£º![]() £¬
£¬
¹Ê![]() £¬
£¬
µ±![]() ʱ£¬¹ư
ʱ£¬¹ư![]() ×÷
×÷![]() Öᣬ
Öᣬ
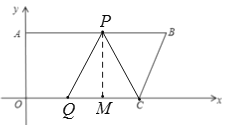
ÓÉ̀ẩâµĂ£º![]() £¬
£¬
Ộ![]() £¬
£¬
½âµĂ£º![]() £¬
£¬
¹Ê![]() .
.

 ͨ³ÇѧµäĬдÄÜÊÖϵÁĐ´đ°¸
ͨ³ÇѧµäĬдÄÜÊÖϵÁĐ´đ°¸¡¾̀âÄ¿¡¿Ä³È˹º½ø̉»ÅúÇíÖĐẦ³Èµ½ÊĐ³¡ÉÏÁăÊÛ£¬̉ÑÖªÂô³öµÄẦ³ÈÊưÁ¿x(ǧ¿Ë)ÓëÊÛ¼Ûy(Ôª)µÄ¹ØϵÈçÏÂ±í£º
ÊưÁ¿x(ǧ¿Ë) | 1 | 2 | 3 | 4 | 5 | ¡ |
ÊÛ¼Ûy(Ôª) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 | ¡ |
(1)Đ´³öÊÛ¼Ûy(Ôª)ÓëẦ³ÈÊưÁ¿x(ǧ¿Ë)Ö®¼äµÄº¯Êư¹Øϵʽ£»
(2)Ơâ¸öÈËÈôÂô³ö50ǧ¿ËµÄẦ³È£¬ÊÛ¼ÛΪ¶àÉÙÔª£¿