题目内容
【题目】如图,直线![]() 与直线
与直线![]() 和直线
和直线![]() 分别交于点
分别交于点![]() (
(![]() 在
在![]() 的上方).
的上方).

![]() 直线
直线![]() 和直线
和直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为 ;
的坐标为 ;
![]() 求线段
求线段![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
![]() 点
点![]() 是
是![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的值及点
的值及点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,且
,且![]() ;(3)当
;(3)当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 点坐标为
点坐标为![]() 或
或![]() ;当
;当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 点坐标为
点坐标为![]() ;当
;当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 点坐标为
点坐标为![]() .
.
【解析】
(1)根据题意联立方程组求解即可.
(2)根据题意,当x=t时,求出D、E点的坐标即可,进而表示DE的长度,注意t的取值范围.
(3)根据等腰三角形的腰的情况分类讨论即可,第一种情况当![]() 时;第二种情况当
时;第二种情况当![]() 时,第三种情况当
时,第三种情况当![]() 时.逐个计算即可.
时.逐个计算即可.
解:![]() 根据题意可得:
根据题意可得:
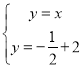
解得:![]()
所以可得Q点的坐标为![]() ;
;
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .
.
![]() 在
在![]() 的上方,
的上方,
![]() ,且
,且![]() .
.
![]()
![]() 为等腰直角三角形.
为等腰直角三角形.
![]() 或
或![]() 或
或![]() .
.
若![]() ,
,![]() 时,
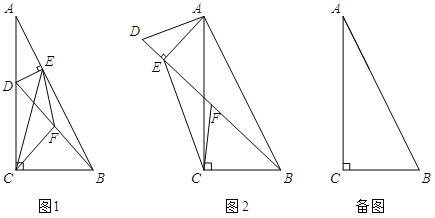
时,![]() ,如图1.解得
,如图1.解得![]() .
.
![]() .
.
![]() 点坐标为
点坐标为![]() .
.
若![]() ,
,![]() 时,如图2,
时,如图2,![]() ,解得
,解得![]() .
.
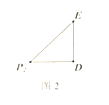
![]() 点坐标为
点坐标为![]() .
.
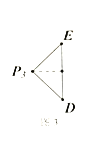
若![]() ,
,![]() 时,即
时,即![]() 为斜边,如图3,可得
为斜边,如图3,可得![]() ,即
,即![]() .解得
.解得![]() .
.
![]() 的中点坐标为
的中点坐标为![]() .
.
![]() 点坐标为
点坐标为![]() .
.
若![]() ,
,![]() 和
和![]() 时,即
时,即![]() ,即
,即![]() ,
,![]() (不符合题意,舍去)
(不符合题意,舍去)
此时直线![]() 不存在.
不存在.
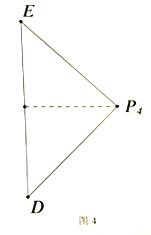
若![]() ,
,![]() 时,如图4,即
时,如图4,即![]() 为斜边,可得
为斜边,可得![]() ,即
,即![]() ,解得
,解得![]() .
.
![]() .
.
![]() 点坐标为
点坐标为![]() .
.
综上所述:当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 点坐标为
点坐标为![]() ;
;
当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 点坐标为
点坐标为![]() ;
;

练习册系列答案
相关题目