题目内容
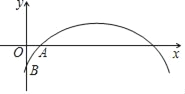
【题目】如图,已知二次函数y1=ax2+bx+c的图象分别与x轴的正半轴、y轴的负半轴于A、B两点,且OA=OB,则一次函数y2=(ac﹣b)x+abc的图象可能是( )
A. 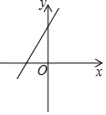 B.
B. 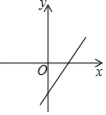 C.
C. 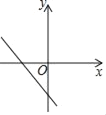 D.
D. 
【答案】D
【解析】
由抛物线的开口向下、对称轴在y轴的右侧且与y轴交点在原点下方知a<0、b>0、c<0,即abc>0,由B(0,c)且OA=OB知点A(-c,0),代入解析式得ac-b=-1<0,据此解答可得.
∵抛物线的开口向下、对称轴在y轴的右侧且与y轴交点在原点下方,
∴a<0、b>0、c<0,
则abc>0,
∵点B(0,c)、且OA=OB,
∴点A(-c,0),
将点A(-c,0)代入解析式,得:ac2-bc+c=0,
∴ac-b=-1<0,
则一次函数y2=(ac-b)x+abc的图象经过第一、二、四象限,
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目