Question

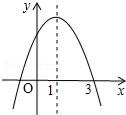
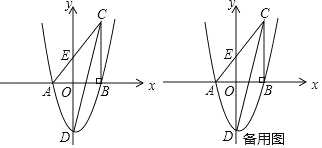
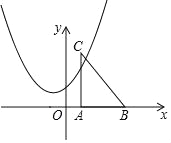
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点C在第一象限，顶点A、B的坐标分别为（1，0），（4，0），∠CAB=90°，BC=5．抛物线y=+bx+c与边AC，y轴的交点的纵坐标分别为3，．

（1）求抛物线y=+bx+c对应的函数关系式；

（2）若将抛物线y=+bx+c经过平移后的抛物线的顶点是边BC的中点，写出平移过程；

（3）若抛物线y=+bx+c平移后得到的抛物线y=+k经过（﹣5，y1），（3，y2）两点，当y1＞y2＞k时，直接写出h的取值范围．

Answer 1

【答案】（1）y=+x+；（2）将y=（x+1）2+1向右平移3.5个单位长度，再向上平移1个单位长度后得到抛物线的顶点是边BC的中点；（3）h的取值范围为h＞﹣1且h≠3

【解析】

（1）根据抛物线y=x2+bx+c与边AC，y轴的交点的纵坐标分别为3，，可得抛物线y=x2+bx+c过点（1，3），（0，），根据待定系数法可求抛物线y=x2+bx+c对应的函数关系式；

（2）根据勾股定理可求AC的长，可得C点坐标，进一步得到BC中点的坐标为（2.5，2），将y=x2+x+配方得y=（x+1）2+1，依此即可写出平移过程；

（3）先求出抛物线y=x2+x+=（x+1）2+1的对称轴为x=-1，可得h的取值范围．

（1）∵抛物线y=+bx+c与边AC，y轴的交点的纵坐标分别为3，．

∴抛物线y=+bx+c过点（1，3），（0，），

把点（1，3），（0，）代入y=+bx+c得．

∴，

∴抛物线y=+bx+c对应的函数关系式为：y=+x+；

（2）在Rt△ABC中，∵∠CAB=90°，AB=4﹣1=3，BC=5，

∴AC=，

∴C（1，4），

∴BC中点的坐标为（2.5，2），

将y=+x+配方得，y=（x+1）2+1，

∴将y=（x+1）2+1向右平移3.5个单位长度，再向上平移1个单位长度后得到抛物线的顶点是边BC的中点；

（3）∵抛物线y=+x+=（x+1）2+1的对称轴为x=﹣1，抛物线y=+bx+c平移后得到的抛物线y=+k经过（﹣5，y1），（3，y2）两点，

∴h的取值范围为h＞﹣1且h≠3．