题目内容
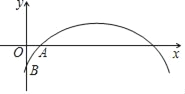
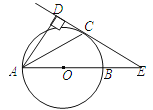
【题目】如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
【答案】(1)证明见解析;
(2),AD=![]() .
.
【解析】
试题(1)连接OC,由AC平分∠DAB得到∠DAC=∠CAB,然后利用等腰三角形的性质得到∠OCA=∠CAB,接着利用平行线的判定得到AD∥CO,而CD⊥AD,由此得到CD⊥AD,最后利用切线的判定定理即可证明CD为⊙O的切线;
(2)由AB=2BO,AB=2BE得到BO=BE=CO,设BO=BE=CO=x,所以OE=2x,在Rt△OCE中,利用勾股定理列出关于x的方程,解方程求出x,最后利用三角函数的定义即可求解.
试题解析:(1)连接OC

∵AC平分∠DAB
∴∠DAC=∠CAB
∵OA=OC
∴∠OCA=∠CAB
∴∠OCA=∠DAC
∴AD∥CO
∵CD⊥AD
∴CD⊥AD
∴CD为⊙O的切线;
(2)∵AB=2BO , AB=2BE
∴BO=BE=CO
设BO=BE=CO=x ,
∴OE=2x
在Rt△OCE中,OC2+CE2=OE2, x2+(![]() )2=(2x)2
)2=(2x)2
∴x=1
∴AE=3 ,∠E=30° ,
∴AD=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】(1) 观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| 0.01 | x | 1 | y | 100 |
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知![]() ≈1.414,则
≈1.414,则![]() =________,
=________,![]() =_______;
=_______;
②![]() = 0.274,记
= 0.274,记![]() 的整数部分为x,则
的整数部分为x,则![]() =___________.
=___________.
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过50kg时,价格均为7元/kg;一次性购买超过50kg时,其中有50kg的价格仍为7元/kg,超过50kg的部分价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为![]() kg(
kg(![]() >0)
>0)
(1)根据题意填表:a= b=
一次购买数量(kg) | 30 | 50 | 150 | … |
甲批发店花费(元) | 180 | 300 | 900 | … |
乙批发店花费(元) | a | 350 | b | … |
(2)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)若小王在同一个批发店一次性购买苹果花费了360元,则他在甲、乙两个批发店中批发,哪个批发店购买数量多?