题目内容
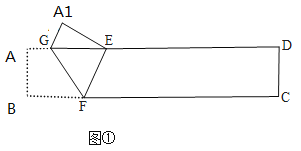
【题目】四边形ABCD是长方形,将长方形ABCD折叠,如图①所示,点B落在AD边上的点E处,折痕为FG,将图②折叠,点C与点E重合,折痕为PH.
(1)在图②中,证明:EH=EP;
(2)若EF=6,EH=8,FH=10,求长方形ABCD的面积.

【答案】(1)见解析;(2)115.2
【解析】
(1)由折叠的性质和平行线的性质得到∠EHP=∠EPH,根据等角对等边即可得到结论;
(2)先证明∠FEH=90°,求出△EFH的面积,由折叠的性质得到BC的长,过E作EM⊥BC于M,根据面积公式求出EM=4.8,然后根据矩形的面积公式即可得出结论.
(1)如图2,由折叠得:∠CHP=∠EHP.
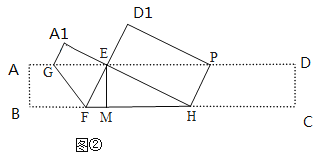
∵EG∥BC,∴∠EPH=∠CHP,
∴∠EHP=∠EPH,
∴EP=EH;
(2)∵![]() ,
,
∴∠FEH=90°,
∴S△EFH=![]() EFEH=24.
EFEH=24.
由折叠得:BF=EF=6 ,CH=EH=8,
∴BC=BF+FH+HC=6+10+8=24.
过E作EM⊥BC于M,
∴S△EFH=![]() FHEM=24,
FHEM=24,
∴FHEM=48.
∵FH=10,
∴EM=4.8,
∴S矩形ABCD=BCEM=115.2.

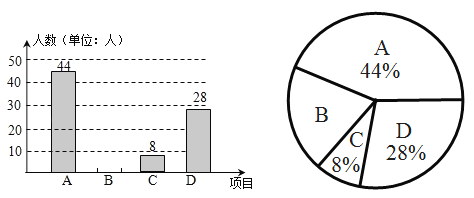
【题目】墨墨和茗茗两人在做抛掷硬币的实验,他们同时各自抛一枚硬币,出现的结果及部分数据如表:
事件 | 两个正面 | 一正一反 | 两个反面 |
频数 |
| ________ |
|
频率 | ________ |
| ________ |
![]() 填写表中空格;
填写表中空格;
![]() 他们各自抛了多少次硬币?
他们各自抛了多少次硬币?
![]() 他们实验的结果可靠吗?说明理由.
他们实验的结果可靠吗?说明理由.
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
【题目】老师组织学生做分组摸球实验.给每组准备了完全相同的实验材料,一个不透明的袋子,袋子中装有除颜色外都相同的3个黄球和若干个白球.先把袋子中的球搅匀后,从中随意摸出一个球,记下球的颜色再放回,即为一次摸球.统计各组实验的结果如下:
一组 | 二组 | 三组 | 四组 | 五组 | 六组 | 七组 | 八组 | 九组 | 十组 | |
摸球的次数 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
摸到白球的次数 | 41 | 39 | 40 | 43 | 38 | 39 | 46 | 41 | 42 | 38 |
请你估计袋子中白球的个数是( )
A.1个B.2个C.3个D.4个