Question

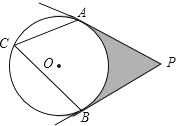
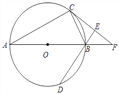
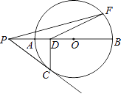
【题目】如图，⊙O中，PC切⊙O于点C，连PO交于⊙O点A、B，点F是⊙O上一点，连PF，CD⊥AB于点D，AD=2，CD=4，则PF：DF的值是（ ）

A. 2 B. C. 5：3 D. 4：3

Answer 1

【答案】C

【解析】

连接AC、OC、OF、BC．由△ADC∽△CDB，推出，求出DB、OA、OD，由△ODC∽△OCP，推出，推出OC2=ODOP，推出OF2=ODOP，即，由∠DOF=∠POF，推出△DOF∽△FOP，可得.

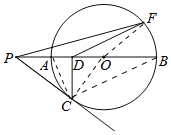
连接AC、OC、OF、BC．如图所示：

∵AB是直径，

∴∠ACB=90°，

∵CD⊥AB，

∴∠ADC=∠BDC=90°，

∴∠ACD+∠CAD=90°，∠ACD+∠BCD=90°，

∴∠CAD=∠BCD，

∴△ADC∽△CDB，

∴，

∴，

∴DB=8，OA=OB=5，OD=3，

∵PC是切线，

∴OC⊥PC，

∵∠DOC=∠POC，∠ODC=∠OCP，

∴△ODC∽△OCP，

∴，

∴OC2=ODOP，

∴OF2=ODOP，

∴，

∵∠DOF=∠POF，

∴△DOF∽△FOP，

∴，

故选：C．