题目内容
【题目】填空并完成以下证明:
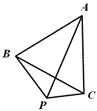
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

【答案】CD,同旁内角互补两直线平行,∠APC,两直线平行内错角相等,∠BAP,∠APC,∠4,内错角相等两直线平行,两直线平行内错角相等
【解析】根据平行线的性质和判定即可解决问题;
∵![]() ,(已知)
,(已知)
∴AB∥CD.(同旁内角互补两直线平行)
∴∠BAP=∠APC.(两直线平行,内错角相等)
又∵∠1=∠2,(已知)
∠3=∠BAP∠1,
∠4=∠APC∠2,
∴∠3=∠4(等式的性质)
∴AE∥PF.(内错角相等两直线平行)
∴∠E=∠F.(两直线平行内错角相等)
故答案为CD,同旁内角互补两直线平行,∠APC,两直线平行内错角相等,∠BAP,∠APC,∠4,内错角相等两直线平行,两直线平行内错角相等;

练习册系列答案
相关题目