题目内容
【题目】如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为( )
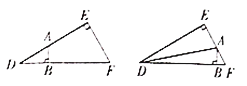

A. (A) B. (B) C. (C) D. (D)
【答案】B
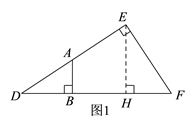
【解析】如图1和图2,过点E作EH⊥DF于点H,
∵在△DEF中,∠DEF=90°,∠D=30°,DF=16,
∴EF=8,DE=![]() ,EH=
,EH=![]() ,DH=12,HF=4,
,DH=12,HF=4,
(1)如图1,当点A在DE上时,此时点B在DH上,即![]() ,
,
∵AB⊥DF于点B,∠D=30°,BD= ![]() ,
,
∴AB=BD·tan∠D= ![]() ,
,
∴此时y=S△ABD= =![]() ,即
,即![]() ,
,
∴当![]() 时,y有最大值,此时点A与E重合;
时,y有最大值,此时点A与E重合;
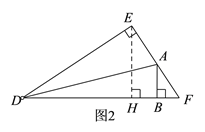
(2)如图2,当点A在EF上时,此时点B在HF上,即![]() ,
,
∵AB⊥DF于点B,∠D=30°,BD= ![]() ,
,
∴BF= ![]() ,∠ABF=90°,∠F=60°,
,∠ABF=90°,∠F=60°,
∴AB=BF·tan∠F=![]() ,
,
∴此时y=S△ABD=![]() BD·AB=
BD·AB=![]() ,即y=
,即y= ![]() ;
;
综上所述,结合二次函数的图象特征可知y随x变化而变化的图象应该是B选项中的图象.
故选B.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目