题目内容
【题目】如图，正方形ABCD的边AB在数轴上，数轴上点A表示的数为﹣1，正方形ABCD的面积为a2（a＞1）．将正方形ABCD在数轴上水平移动，移动后的正方形记为A′B′C′D′，点A、B、C、D的对应点分别为A′、B′、C′、D′，移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S．当S＝a时，数轴上点A′表示的数是_____．（用含a的代数式表示）
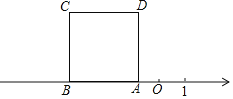
【答案】﹣a或a﹣2
【解析】
根据正方形的面积可得边长进而可以表示点A′表示的数．
∵正方形ABCD的面积为a2（a＞1）．
∴边长为a，
当S＝a时，分两种情况：
若正方形ABCD向左平移，如图1，
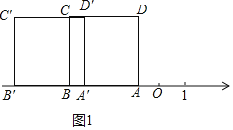
A′B′＝AB＝BC＝a，
A′B＝1，
∴AA′＝AB﹣A′B＝a﹣1，
∴OA′＝OA+AA′＝1+a﹣1＝a，
∴数轴上点A′表示的数为﹣a；
如正方形ABCD向右平移，如图2，
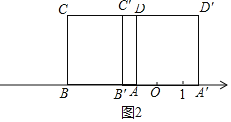
AB′＝1，AA′＝a﹣1，
∴OA′＝（a﹣1）﹣1＝a﹣2
∴数轴上点A′表示的数为a﹣2．
综上所述，数轴上点A′表示的数为﹣a或a﹣2．
练习册系列答案
中考解读考点精练系列答案
相关题目
