题目内容
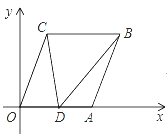
【题目】如图,已知点A(6,0),B(8,5),将线段OA平移至CB,点D(x,0)在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)△ODC与△ABD的面积分别记为S1,S2,设S=S1﹣S2,求S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等,如果存在,请求出x的值(或取值范围);如果不存在,请说明理由.
【答案】(1)![]() ;(2)D(x,0)(x>6)
;(2)D(x,0)(x>6)
【解析】
(1)根据平移的性质可以求得点C的坐标,然后根据两点间的距离公式即可求得AC的长;
(2)根据题意,可以分别表示出S1,S2,从而可以得到S关于x的函数解析式,由图和题目中的条件可以求得△CDB的面积,从而可以求得满足条件的点D的坐标,本题得以解决.
(1)由题意知,将线段OA平移至CB,
∴四边形OABC为平行四边形.
又∵A(6,0),B(8,5),∴点C(2,5).
过点C作CE⊥OA于E,连接AC,在Rt△CEA中,

AC=![]() =
=![]() =
=![]() .
.
(2)∵点D的坐标为(x,0),
若点D在线段OA上,即当0<x<6时,
![]() ,
,![]() ,
,
∴![]() =5x-15.
=5x-15.
若点D在OA的延长线上,即当x>6时,
![]() ,
,![]() ,
,
∴![]() =15.
=15.
由上可得,![]()
∵![]() ,
,
当0<x<6时,![]() 时,x=6(与A重合,不合题意,舍去);
时,x=6(与A重合,不合题意,舍去);
当x>6时,![]() ,点D在OA延长线上的任意一点处都可满足条件,
,点D在OA延长线上的任意一点处都可满足条件,
∴点D所在位置为D(x,0)(x>6).

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.