ĢāÄæÄŚČŻ
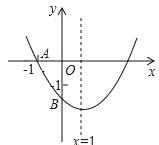
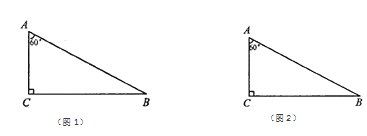
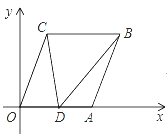
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßC1£ŗy=ax2+bx©a2¹ŲÓŚyÖį¶Ō³ĘĒŅÓŠ×īŠ”Öµ©1£®
£Ø1£©ĒóÅ×ĪļĻßC1µÄ½āĪöŹ½£»
£Ø2£©ŌŚĶ¼1ÖŠÅ×ĪļĻßC1¶„µćĪŖA£¬½«Å×ĪļĻßC1ČĘ µćBŠż×Ŗ180”ćŗóµĆµ½Å×ĪļĻßC2£¬Ö±Ļßy=kx©2k+4×ܾ¹żŅ»¶ØµćM£¬Čō¹ż¶ØµćMµÄÖ±ĻßÓėÅ×ĪļĻßC2Ö»ÓŠŅ»øö¹«¹²µć£¬ĒóÖ±ĻßlµÄ½āĪöŹ½£®
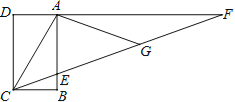
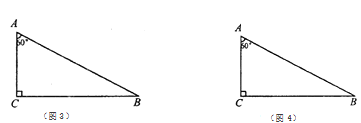
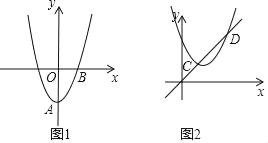
£Ø3£©ČēĶ¼2£¬ĻČ½«Å×ĪļĻß C1ĻņÉĻĘ½ŅĘŹ¹Ę䶄µćŌŚŌµćO£¬ŌŁ½«Ę䶄µćŃŲÖ±Ļßy=xĘ½ŅʵƵ½Å×ĪļĻßC3£¬ÉčÅ×ĪļĻßC3ÓėÖ±Ļßy=x½»ÓŚC”¢DĮ½µć£¬ĒóĻ߶ĪCDµÄ³¤£®
”¾“š°ø”æ£Ø1£©y=x2©1£Ø2£©¹ż¶ØµćM£¬¹²ÓŠČżĢõÖ±Ļßl£ŗx=2 »ņy=2![]() x+4©4
x+4©4![]() »ņy=©2
»ņy=©2![]() x+4+4
x+4+4![]() £¬ĖüĆĒ·Ö±šÓėÅ×ĪļĻßC3Ö»ÓŠŅ»øö¹«¹²µć£Ø3£©
£¬ĖüĆĒ·Ö±šÓėÅ×ĪļĻßC3Ö»ÓŠŅ»øö¹«¹²µć£Ø3£©![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ ![]() øł¾ŻÅ×ĪļĻߵĶŌ³ĘÖįĪŖ
øł¾ŻÅ×ĪļĻߵĶŌ³ĘÖįĪŖ![]() Öį£¬ĒóµĆ
Öį£¬ĒóµĆ![]() Å×ĪļĻßÓŠ×īŠ”Öµ£¬æÉĒóµĆ
Å×ĪļĻßÓŠ×īŠ”Öµ£¬æÉĒóµĆ![]() £¬¼“æÉĒó³öÅ×ĪļĻß
£¬¼“æÉĒó³öÅ×ĪļĻß![]() µÄ½āĪöŹ½.
µÄ½āĪöŹ½.
![]() ŅĄĢāŅāæÉĒó³öÅ×ĪļĻß
ŅĄĢāŅāæÉĒó³öÅ×ĪļĻß![]() µÄ½āĪöŹ½ĪŖ£ŗ
µÄ½āĪöŹ½ĪŖ£ŗ ![]() ÓÉÖ±Ļß
ÓÉÖ±Ļß![]() ×ܾ¹żŅ»¶ØµćM£¬æÉĒóµĆ¶ØµćMĪŖ
×ܾ¹żŅ»¶ØµćM£¬æÉĒóµĆ¶ØµćMĪŖ![]() £¬¢Ł¾¹ż¶Øµć
£¬¢Ł¾¹ż¶Øµć![]() Óė
Óė![]() ÖįĘ½ŠŠµÄÖ±Ļß
ÖįĘ½ŠŠµÄÖ±Ļß![]() £ŗ
£ŗ ![]() ÓėÅ×ĪļĻß
ÓėÅ×ĪļĻß![]() ×ÜÓŠŅ»øö¹«¹²µć
×ÜÓŠŅ»øö¹«¹²µć![]() £®¢Ś¾¹ż¶Øµć
£®¢Ś¾¹ż¶Øµć![]() µÄÖ±Ļß
µÄÖ±Ļß![]() ĪŖŅ»“ĪŗÆŹż
ĪŖŅ»“ĪŗÆŹż![]() Ź±£¬Óė
Ź±£¬Óė![]() ĮŖĮ¢·½³Ģ×飬ĄūÓĆ
ĮŖĮ¢·½³Ģ×飬ĄūÓĆ![]() æɵƵĆ
æɵƵĆ![]() µÄÖµ£¬¼“æÉµĆ³ö
µÄÖµ£¬¼“æÉµĆ³ö![]() »ņ
»ņ![]() £¬×ŪÉĻĖłŹö£¬¹ż¶ØµćM£¬¹²ÓŠČżĢõÖ±ĻßĖüĆĒ·Ö±šÓėÅ×ĪļĻß
£¬×ŪÉĻĖłŹö£¬¹ż¶ØµćM£¬¹²ÓŠČżĢõÖ±ĻßĖüĆĒ·Ö±šÓėÅ×ĪļĻß![]() Ö»ÓŠŅ»øö¹«¹²µć£®
Ö»ÓŠŅ»øö¹«¹²µć£®
![]() ÉčÅ×ĪļĻß
ÉčÅ×ĪļĻß![]() µÄ¶„µćĪŖ
µÄ¶„µćĪŖ![]() £¬ŅĄĢāŅāæɵĆÅ×ĪļĻß
£¬ŅĄĢāŅāæɵĆÅ×ĪļĻß![]() µÄ½āĪöŹ½ĪŖ£ŗ
µÄ½āĪöŹ½ĪŖ£ŗ ![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() ĮŖĮ¢£¬æɵĆ
ĮŖĮ¢£¬æɵĆ![]() µÄ×ų±ź£¬¹żµćC×÷
µÄ×ų±ź£¬¹żµćC×÷![]() ”Ī
”Ī![]() Öį£¬¹żµćD×÷DM”ĪyÖį£¬æÉĒó³ö
Öį£¬¹żµćD×÷DM”ĪyÖį£¬æÉĒó³ö![]() ¼“æÉµĆ³ö
¼“æÉµĆ³ö![]() µÄÖµ£®
µÄÖµ£®
ŹŌĢā½āĪö£ŗ£Ø1£©![]() Å×ĪļĻߵĶŌ³ĘÖįĪŖ
Å×ĪļĻߵĶŌ³ĘÖįĪŖ![]() Öį£¬
Öį£¬
![]() ½āµĆ
½āµĆ![]()
![]() Å×ĪļĻߵĽāĪöŹ½ĪŖ
Å×ĪļĻߵĽāĪöŹ½ĪŖ![]()
![]() µ±
µ±![]() Å×ĪļĻßÓŠ×īŠ”Öµ£¬¼“
Å×ĪļĻßÓŠ×īŠ”Öµ£¬¼“![]() ½āµĆ£ŗ
½āµĆ£ŗ ![]() »ņ
»ņ![]() £ØÉįČ„£©£®
£ØÉįČ„£©£®
Å×ĪļĻß![]() µÄ½āĪöŹ½
µÄ½āĪöŹ½![]()
£Ø2£©Å×ĪļĻß![]() µÄ½āĪöŹ½
µÄ½āĪöŹ½![]()
![]()
ÉčÅ×ĪļĻß![]() ÓėxÖįµÄĮīŅ»øö½»µćĪŖ
ÓėxÖįµÄĮīŅ»øö½»µćĪŖ![]() £®
£®
Įī![]() µĆ£ŗ
µĆ£ŗ ![]() ½āµĆ£ŗ
½āµĆ£ŗ ![]()
![]()
½«Å×ĪļĻß![]() Čʵć
Čʵć![]() Šż×Ŗ
Šż×Ŗ![]() ŗóµĆµ½Å×ĪļĻß
ŗóµĆµ½Å×ĪļĻß![]() £¬
£¬
”ąµć![]() ¶ŌÓ¦µćµÄ×ų±źĪŖ
¶ŌÓ¦µćµÄ×ų±źĪŖ![]() £¬µć
£¬µć![]() ¶ŌÓ¦µćµÄ×ų±źĪŖ
¶ŌÓ¦µćµÄ×ų±źĪŖ![]() .
.
Éč![]() µÄ½āĪöŹ½ĪŖ
µÄ½āĪöŹ½ĪŖ![]() ½«
½«![]() “śČėµĆ£ŗ
“śČėµĆ£ŗ ![]() ½āµĆ
½āµĆ![]()
![]() µÄ½āĪöŹ½ĪŖ
µÄ½āĪöŹ½ĪŖ![]()
Ö±Ļß![]() ×ܾ¹żŅ»¶ØµćM£¬
×ܾ¹żŅ»¶ØµćM£¬
”ą¶ØµćMĪŖ![]() £¬
£¬
¢Ł¾¹ż¶Øµć![]() Óė
Óė![]() ÖįĘ½ŠŠµÄÖ±Ļß
ÖįĘ½ŠŠµÄÖ±Ļß![]() £ŗ
£ŗ ![]() ÓėÅ×ĪļĻß
ÓėÅ×ĪļĻß![]() ×ÜÓŠŅ»øö¹«¹²µć
×ÜÓŠŅ»øö¹«¹²µć![]() £®
£®
¢Ś½«![]() Óė
Óė![]() ĮŖĮ¢µĆ£ŗ
ĮŖĮ¢µĆ£ŗ ![]() ÕūĄķµĆ£ŗ
ÕūĄķµĆ£ŗ ![]()
”ß¹ż¶ØµćMµÄÖ±ĻßÓėÅ×ĪļĻß![]() Ö»ÓŠŅ»øö¹«¹²µć£¬
Ö»ÓŠŅ»øö¹«¹²µć£¬
![]() ½āµĆ
½āµĆ![]()
”ą¹ż¶ØµćMµÄÖ±ĻߵĽāĪöŹ½ĪŖ![]() »ņ
»ņ![]() £¬
£¬
×ŪÉĻĖłŹö£¬¹ż¶ØµćM£¬¹²ÓŠČżĢõÖ±Ļßl£ŗ ![]() »ņ
»ņ![]() »ņ
»ņ![]() £¬ĖüĆĒ·Ö±šÓėÅ×ĪļĻß
£¬ĖüĆĒ·Ö±šÓėÅ×ĪļĻß![]() Ö»ÓŠŅ»øö¹«¹²µć£®
Ö»ÓŠŅ»øö¹«¹²µć£®
£Ø3£©ŅŌĘ½ŅĘŗóÅ×ĪļĻߵĶ„µćĪŖ×ų±źŌµć½ØĮ¢×ų±źĻµ£¬ŌņÖ±ĻßŗĶÅ×ĪļĻßŌŚŠĀ×ų±źĻµµÄ½āĪöŹ½ĪŖ![]() Óė
Óė![]()
½«![]() Óė
Óė![]() ĮŖĮ¢£¬½āµĆ£ŗ
ĮŖĮ¢£¬½āµĆ£ŗ ![]() »ņ
»ņ![]()
”ąµć![]() ŗĶµć
ŗĶµć![]() ŌŚŠĀ×ų±źĻµÄŚµÄ×ų±ź·Ö±šĪŖ
ŌŚŠĀ×ų±źĻµÄŚµÄ×ų±ź·Ö±šĪŖ![]()
![]()