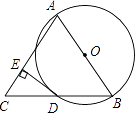题目内容
【题目】如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= ![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④ ![]() 为定值.其中一定成立的是 .
为定值.其中一定成立的是 .
【答案】①②③④
【解析】解:如图1所示:
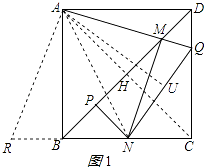
作AU⊥NQ于U,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN,故①正确.
由同角的余角相等知,∠HAM=∠PMN,
在△AHM和△MPN中,
 ,
,
∴△AHM≌△MPN(AAS),
∴MP=AH= ![]() AC=
AC= ![]() BD,故②正确,
BD,故②正确,
∵∠BAN+∠QAD=∠NAQ=45°,
∴△ADQ绕点A顺时针旋转90度至△ABR,使AD和AB重合,连接AN,
则∠RAQ=90°,△ABR≌△ADQ,
∴AR=AQ,∠RAN=90°﹣45°=45°=∠NAM,
在△AQN和△ANR中,
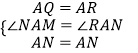 ,
,
∴△AQN≌△ANR(SAS),
∴NR=NQ,
则BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ,故③正确.
如图2所示,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
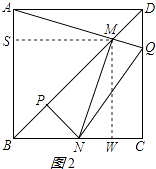
∴四边形SMWB是正方形,
∴MS=MW=BS=BW,∠SMW=90°,
∴∠AMS=∠NMW,
在△AMS和△NMW中,
 ,
,
∴△AMS≌△NMW(ASA),
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1: ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,故④正确.
,故④正确.
所以答案是:①②③④.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】2018年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对,正确处置,顺利返航,避免了一场灾难的发生,创造了世界航空史上的奇迹!下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表,请回答以下几个问题:
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度(℃) | 20 | 14 | 8 | 2 |
|
(1)上表反映的两个变量中,______是自变量,______是因变量.
(2)若用h表示距离地面的高度,用y表示表示温度,则y与h的之间的关系式是:__________;
当距离地面高度5千米时,所在位置的温度为:_________℃.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用时间关系图.根据图象回答以下问题:
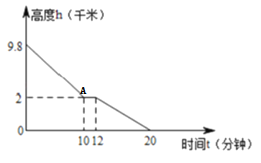
(3)点A表示的意义是什么?返回途中飞机在2千米高空水平大约盘旋了几分钟?
(4)飞机发生事故时所在高空的温度是多少?