题目内容
已知抛物线y=a(x-m)
2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)如图1,求抛物线y=(x-2)
2+1的伴随直线的解析式.
(2)如图2,若抛物线y=a(x-m)
2+n(m>0)的伴随直线是y=x-3,伴随四边形的面积为12,求此抛物线的解析式.
(3)如图3,若抛物线y=a(x-m)
2+n的伴随直线是y=-2x+b(b>0),且伴随四边形ABCD是矩形.
①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
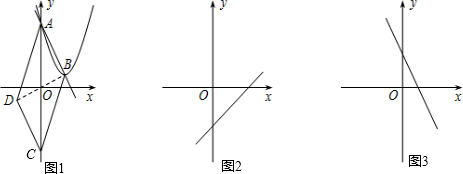
分析:(1)利用抛物线y=(x-2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),求出直线解析式即可;
(2)首先得出点A的坐标为(0,-3),以及点C的坐标为(0,3),进而求出BE=2,得出顶点B的坐标求出解析式即可;
(3)①由已知可得A坐标为(0,b),C点坐标为(0,-b),以及n=-2m+b,即点B点的坐标为(m,-2m+b),利用勾股定理求出;
②利用①中B点坐标,以及BD的长度即可得出P点的坐标.
解答:解:(1)由抛物线y=a(x-m)
2+n与y轴交于点A,它的顶点为点B,
∴抛物线y=(x-2)
2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),
设所求直线解析式为y=kx+b,
∴
,
解得:
,
∴所求直线解析式为y=-2x+5;
(2)如图,作BE⊥AC于点E,由题意得四边形ABCD是平行四边形,点A的坐标为(0,-3),
点C的坐标为(0,3),
可得:AC=6,
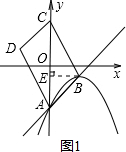
∵平行四边形ABCD的面积为12,
∴S
△ABC=6即S
△ABC=
AC•BE=6,
∴BE=2,
∵m>0,即顶点B在y轴的右侧,且在直线y=x-3上,
∴顶点B的坐标为(2,-1),
又抛物线经过点A(0,-3),
∴a=-
,
∴y=-
(x-2)
2-1;
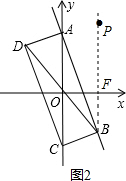
(3)①如图,作BF⊥x轴于点F,
由已知可得A坐标为(0,b),C点坐标为(0,-b),
∵顶点B(m,n)在直线y=-2x+b(b>0)上,
∴n=-2m+b,即点B点的坐标为(m,-2m+b),
在矩形ABCD中,CO=BO.
∴b=
,
∴b
2=m
2+4m
2-4mb+b
2,
∴m=
b,
n=-2×
b+b=-
b,
②∵B点坐标为(m,n),即(
b,-
b),
∴BO=
=b,
∴BD=2b,
当BD=BP,
∴PF=2b-
b=
b,
∴P点的坐标为(
b,
b);
如图3,当DP=PB时,
过点D作DE⊥PB,于点E,
∵B点坐标为(
b,-
b),
∴D点坐标为(-
b,
b),
∴DE=
b,BE=
b,设PE=x,
∴DP=PB=
b+x,
∴DE
2+PE
2=DP
2,
∴
(b)2+x
2=(
b+x)
2,
解得:x=
b,
∴PF=PE+EF=
b+
b=
b,
∴此时P点坐标为:(
b,
b);
同理P可以为(
b,-
b);(
b,
b),
故P点坐标为:(
b,
b);(
b,
b);(
b,-
b);(
b,
b).
点评:此题主要考查了二次函数的综合应用以及勾股定理和点的坐标性质,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
练习册系列答案
相关题目








 名校课堂系列答案
名校课堂系列答案 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-