题目内容
 已知:如图,AB为⊙O的直径,C是⊙O上一点,过点C的切线与AB的延长线相交于点E,AD⊥EC,垂足为D,且AD交⊙O于点F.
已知:如图,AB为⊙O的直径,C是⊙O上一点,过点C的切线与AB的延长线相交于点E,AD⊥EC,垂足为D,且AD交⊙O于点F.
求证:(1)弧BC=弧CF;
(2)EC•CD=EB•DA.
证明:(1) 连接OC,
连接OC,
∵CD是圆的切线,
∴OC⊥CD,
∵AD⊥EC,
∴AD∥OC,
∴∠OCA=∠CAD,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠CAD,
∴弧BC=弧CF;
(2)连接BC,
∵ED是圆的切线,
∴∠BCE=∠A,
∵∠E=∠E,
∴△EBC∽△ECA,
∴EB:EC=AC:AB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴△ACB∽△ADC,
∴AD:CD=AC:AB,
∴EB:EC=AD:CD
∴EC•CD=EB•DA.
分析:(1)若证明弧BC=弧CF,则可转化为证明∠BAC=∠CAD即可;
(2)连接CB,证明△EBC
点评:本题考查圆的切线的性质、圆周角定理、相似三角形的判定和性质以及比例式的证明方法,题目的综合性较强,难度中等.
 连接OC,
连接OC,∵CD是圆的切线,
∴OC⊥CD,
∵AD⊥EC,
∴AD∥OC,
∴∠OCA=∠CAD,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠CAD,
∴弧BC=弧CF;
(2)连接BC,
∵ED是圆的切线,
∴∠BCE=∠A,
∵∠E=∠E,
∴△EBC∽△ECA,
∴EB:EC=AC:AB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴△ACB∽△ADC,
∴AD:CD=AC:AB,
∴EB:EC=AD:CD
∴EC•CD=EB•DA.
分析:(1)若证明弧BC=弧CF,则可转化为证明∠BAC=∠CAD即可;
(2)连接CB,证明△EBC
点评:本题考查圆的切线的性质、圆周角定理、相似三角形的判定和性质以及比例式的证明方法,题目的综合性较强,难度中等.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA= 已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°. 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为 已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
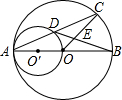 已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.