题目内容
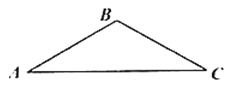
【题目】如图,D 是△ABC 的 BC 边上一点,AB 10,AD 6,DC 2AD,![]() .
.
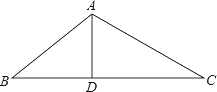
(1)求 AC 的长;
(2)求△ABC 的面积.
【答案】(1)![]() (2)60
(2)60![]()
【解析】
(1)由DC=2AD,根据AD的长求出DC的长,进而求出BD的长,在三角形ABD中,由AB,AD以及BD的长,利用勾股定理的逆定理判断得到三角形为直角三角形,运用勾股定理即可求AC的长.
(2)求BC的长,运用三角形的面积公式即可求出三角形ABC面积.
(1)∵AD=6,DC=2AD,
∴DC=12,
∵![]() ,
,
∴BD=8
在△ABD中,AB=10,AD=6,BD=8,
∵AB2=AD2+BD2,
∴△ABD为直角三角形,即AD⊥BC,
∴AC2= AD2+CD2=180
∴AC=![]()
(2)由(1)得:AD⊥BC
∵BC=BD+DC=8+12=20,AD=6,
∴S△ABC=![]() ×20×6=60.
×20×6=60.

练习册系列答案
相关题目
【题目】如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
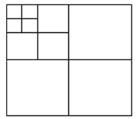
(1)填表
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
(2)如果剪n次,共剪出多少个小正方形?
(3)能否经过若干次分割后共得到2019片纸片?若能,请直接写出相应的次数,若不能,请说明理由.