题目内容
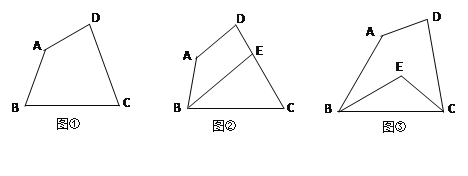
【题目】四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【答案】(1)70°;(2)60°;(3)110°
【解析】
(1)根据四边形的内角和是360°,结合已知条件就可求解;
(2)根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,进一步根据四边形的内角和定理进行求解;
(3)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB的度数,再进一步求得∠BEC的度数.
(1)在四边形ABCD中,
∵∠A+∠B+∠C+∠D=360°, 又∠A=140°,∠D=80°,∠B=∠C,
∴140°+∠C+∠C+80°=360°,即∠C=70°.
(2)∵BE∥AD,∠A=140°,∠D=80°,
∴∠BEC=∠D,∠A+∠ABE=180°.
∴∠BEC=80°,∠ABE=40°.
∵BE是∠ABC的平分线,
∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
(3)在四边形ABCD中, 有∠A+∠ABC+∠BCD+∠D=360°, ∠A=140°,∠D=80°,
所以∠ABC+∠BCD=140°,从而有![]() ∠ABC+
∠ABC+![]() ∠BCD=70°.
∠BCD=70°.
因为∠ABC和∠BCD的角平分线交于点E,所以有∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD.
∠BCD.
故∠C=180°-(∠EBC +∠ECB)=180°-(![]() ∠ABC+
∠ABC+![]() ∠BCD)=180°-70°=110°.
∠BCD)=180°-70°=110°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目