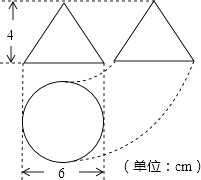
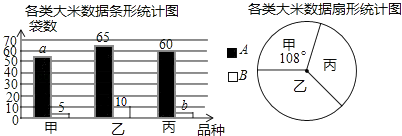
��Ŀ����
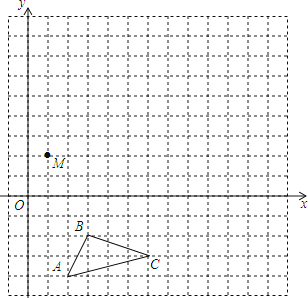
����Ŀ����ͼ��ƽ��ֱ������ϵ�ڣ�С����������ı߳�Ϊ1����λ���ȣ���ABC���������������ֱ�ΪA����1��3����B����4��0����C��0��0��
��1����������ABC����ƽ��1����λ���ȣ�������ƽ��5����λ���Ⱥ�õ��ġ�A1B1C1��
��2����������ABC��ԭ��O˳ʱ�뷽����ת90��õ���A2B2O��
��3����x���ϴ���һ��P�������P��A1���A2����֮����С����ֱ��д��P������꣮
���𰸡�
��1���⣺��ͼ��ʾ����A1B1C1Ϊ�������������Σ�
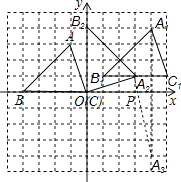
��2���⣺��ͼ��ʾ����A2B2OΪ�������������Σ�

��3���⣺��A2����Ϊ��3��1����A3����Ϊ��4����4����
��A2A3����ֱ�ߵĽ���ʽΪ��y=��5x+16��
��y=0����x= ![]() ��
��
��P������꣨ ![]() ��0����
��0����
�����������⿼����������ת��ƽ�Ʊ任��ͼ��������������ṹȷ�ҳ���Ӧ���λ���ǽ���Ĺؼ�����1���ֱ�A��B��C����ƽ��1����λ��������ƽ��5����λ��Ȼ��˳�����ӣ���2����������ṹ�ҳ���A��B��C�Ե�OΪ��ת����˳ʱ����ת90���Ķ�Ӧ�㣬Ȼ��˳�����Ӽ��ɣ���3���������·����������������A1�����x��ĶԳƵ�A3 �� ������A2A3��x��Ľ��㼴Ϊ����

����Ŀ���±���ӳ����ij�������ʹ����x��ǧ��ʱ����Ӧ�����y��Ԫ��֮��Ĺ�ϵ������˵������ȷ���ǣ�������
�õ���x��ǧ��ʱ�� | 1 | 2 | 3 | 4 | �� |
��Ӧ�����y��Ԫ�� | ��0.55 | ��1.1 | ��1.65 | ��2.2 | ���� |
A. x��y���DZ�������x���Ա�����y��x�ĺ���
B. �õ���ÿ����1ǧ��ʱ���������0.55Ԫ
C. �������20.5Ԫʱ���õ���Ϊ37ǧ��ʱ
D. ���õ���Ϊ8ǧ��ʱ����Ӧ�����4.4Ԫ