题目内容
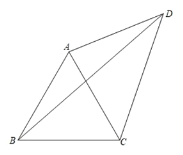
【题目】如图，△ABC中，AB=BC,∠ABC=120°，点E是AC上一点，连接BE，且∠BEC=50°，D为点B关于直线AC的对称点，连接CD，将线段EB绕点E顺时针旋转40°得到线段EF，连接DF.
（1）请你在下图中补全图形；
（2）请写出∠EFD的大小，并说明理由；
（3）连接CF,求证：DF=CF.
【答案】（1）图见解析；（2）60°；理由见解析；（3）见解析.
【解析】
（1）根据题意补全图形即可；
（2）连接ED，根据对称性质可得：ED=EB，∠BEC=∠DEC=50°，再根据旋转性质可得：BE=EF，∠BEF=40°，从而得出EF=ED，∠FED=∠BEC＋∠DEC－∠BEF=60°，即可判定△EFD为等边三角形，从而求出∠EFD的大小；
（3）连接BF并延长交DC于G，利用等边对等角求出∠BCA，根据对称的性质可得：CB=CD，∠BCG=2∠BAC=2∠DCA=60°,再求出∠CBG的度数，从而可判定BG⊥CD，再根据30°所对的直角边是斜边的一半，即可证出G是CD的中点，从而得到BG垂直平分CD，根据垂直平分线的性质即可证DF=CF.
补全图形如下所示：
（2）连接ED，
∵D为点B关于直线AC的对称点
∴ED=EB，∠BEC=∠DEC=50°
∵EB绕点E顺时针旋转40°得到线段EF
∴BE=EF，∠BEF=40°
∴EF=ED，∠FED=∠BEC＋∠DEC－∠BEF=60°
∴△EFD为等边三角形
∴∠EFD=60°
（3）连接BF并延长交DC于G
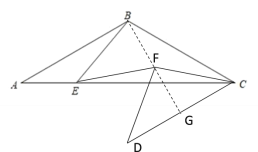
∵AB=AC，∠ABC=120°
∴∠A=∠BCA=
（180°－∠ABC）=30°
∵D为点B关于直线AC的对称点
∴CB=CD，∠BCG=2∠BAC=2∠DCA=60°
∵BE=EF，∠BEF=40°
∴∠EBF=∠EFB=（180°－∠BEF）=70°
∠EBC=180°－∠BEC－∠BCE=100°
∴∠CBG=∠EBC－∠EBF=30°
∴∠BGC=180°－∠CBG－∠BCG=90°
∴BG⊥CD，CG=BC=CD
∴G为CD的中点
∴BG垂直平分CD
∴DF=CF.
