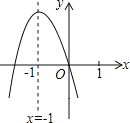题目内容
【题目】如图，以等边△ABC的边AC为腰作等腰△CAD,使AC=AD,连接BD,若∠DBC=41°，∠CAD=________°.
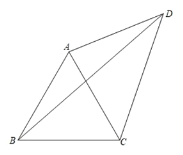
【答案】82°
【解析】
根据等边三角形的性质可得：AB=AC，∠ABC=∠BAC=60°，从而求出∠ABD的度数，然后根据已知条件可得：AB= AD，根据等边对等角即可得：∠ADB=∠ABD，利用三角形的内角和即可求出∠BAD，从而求出∠CAD的度数.
解：∵△ABC是等边三角形
∴AB=AC，∠ABC=∠BAC=60°
∵AC=AD，∠DBC=41°
∴AB= AD，∠ABD=∠ABC－∠DBC=19°
∴∠ADB=∠ABD=19°
∴∠BAD=180°－∠ADB－∠ABD=142°
∴∠CAD=∠BAD－∠BAC=82°
故答案为：82°.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某“数学兴趣小组”根据学习函数的经验，对函数
的图象和性质进行了探究，探究过程如下，请补充完整：
（1）自变量x的取值范围是全体实数，x与y的几组对应数值如下表：
x | … | －3 | － | －2 | －1 | 0 | 1 | 2 |
| 3 | … |
y | … | －2 | － | m | 2 | 1 | 2 | 1 | － | －2 | … |
其中m=____________；
（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）根据函数图象
①写出该函数的一条性质_______________；
②直线
经过点（－l，2），若关于x的方程
有4个互不相等的实数根，则b的取值范围是__________________.
