Question

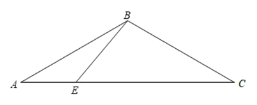
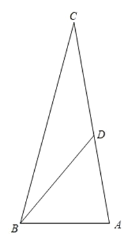
【题目】在△ABC的边AC上取一点，使得AB=AD,若点D恰好在BC的垂直平分线上，写出∠ABC与∠C的数量关系，并证明.

Answer 1

【答案】∠ABC =3∠C，理由见解析.

【解析】

根据等边对等角即可得：∠ABD=∠ADB，然后根据垂直平分线的性质可得：DB=DC，再根据等边对等角即可得：∠DBC=∠C，根据三角形外角的性质，可得∠ADB=∠DBC＋∠C=2∠C，从而得到∠ABD=2∠C，即可得到∠ABC与∠C的数量关系.

解：∠ABC =3∠C，理由如下：

∵AB=AD

∴∠ABD=∠ADB

∵点D恰好在BC的垂直平分线上

∴DB=DC

∴∠DBC=∠C

∴∠ADB=∠DBC＋∠C=2∠C

∴∠ABD=2∠C

∴∠ABC=∠ABD＋∠CBD=2∠C＋∠C=3∠C