题目内容
【题目】体育场上，老师用绳子围成一个周长为
的游戏场地，围成的场地是如图所示的矩形
，设
的长为
（
取整数），矩形
的面积为
.
⑴.写出
与
之间的函数关系式，求出
的最值和相应的
的值；
⑵.若矩形
的面积为
且
,请求出此时
的长.
【答案】（1）
；当
时， 
的最大值
.（2）5.
【解析】试题分析：（1）根据矩形的面积公式列出函数关系式，根据二次函数的性质解决即可；（2）令S=50，解方程即可.
试题解析：
⑴.根据矩形的面积求法可列：
， 整理为: 
，
∴对称轴为
.∵
，按理说
时， 
的值最大.
但由于“
取整数”，所以根据二次函数的性质：当
，在对称轴的左侧
随
的增大而增大；所以应该在
范围来取
的最大整数值，代入来求“
的最大值”.
当
时， 
的最大值
.
⑵.当
时， 
,
解得： 
.
∵矩形
周长为
,
∴img src="http://thumb.zyjl.cn/questionBank/Upload/2018/10/02/10/efc8742d/SYS201810021005553090752458_DA/SYS201810021005553090752458_DA.026.png" width="128" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ,
∴当
即
时， 
；当
即
时， 
.
∵
∴
.
新辅教导学系列答案
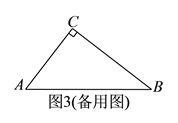
阳光同学一线名师全优好卷系列答案【题目】（
分）如图，在
中， 
， 
， 
，点
在边
上运动， 
平分
交边
于点
， 
垂足为
， 
垂足为
．
（
）当
时，求证： 
．
（
）探究： 
为何值时， 
与
相似？
（
）直接写出： 
__________时，四边形
与
的面积相等．
【题目】“立定跳远”是我市初中毕业生体育测试项目之一．测试时，记录下学生立定跳远的成绩，然后按照评分标准转化为相应的分数，满分10分．其中男生立定跳远的评分标准如下：注：成绩栏里的每个范围，含最低值，不含最高值．
成绩（米） | … | 1.80～1.86 | 1.86～1.94 | 1.94～2.02 | 2.02～2.18 | 2.18～2.34 | 2.34～ |
得分（分） | … | 5 | 6 | 7 | 8 | 9 | 10 |
某校九年级有480名男生参加立定跳远测试，现从中随机抽取10名男生测试成绩（单位：分）如下：
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题：
（1）求这10名男生立定跳远成绩的极差和平均数；
（2）求这10名男生立定跳远得分的中位数和众数；
（3）如果将9分（含9分）以上定为“优秀”，请你估计这480名男生中得优秀的人数．
