题目内容
【题目】如图1,等腰△ABC中,AC=BC=![]() , ∠ACB=45,AO是BC边上的高,D为线段AO上一动点,以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45,连结BE.
, ∠ACB=45,AO是BC边上的高,D为线段AO上一动点,以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45,连结BE.
(1) 求证:△ACD≌△BCE;
(2) 如图2,在图1的基础上,延长BE至Q, P为BQ上一点,连结CP、CQ,若CP=CQ=5,求PQ的长.
(3) 连接OE,直接写出线段OE的最小值.


【答案】(1)证明见解析;(2)PQ=6;(3)OE=![]()
【解析】试题分析: ![]() 根据
根据![]() 即可证得
即可证得![]()
![]() 首先过点
首先过点![]() 作
作![]() 于
于![]() ,由等腰三角形的性质,即可求得
,由等腰三角形的性质,即可求得![]() 则根据等腰三角形与直角三角形中的勾股定理即可求得
则根据等腰三角形与直角三角形中的勾股定理即可求得![]() 的长.
的长.
![]()
![]() 时,
时, ![]() 取得最小值.
取得最小值.
试题解析: ![]() 证明:∵△ABC与△DCE是等腰三角形,
证明:∵△ABC与△DCE是等腰三角形,
∴AC=BC,DC=EC, ![]()
![]()
∴∠ACD=∠BCE;
在△ACD和△BCE中,

![]()
![]() 首先过点
首先过点![]() 作
作![]() 于
于![]() ,
,
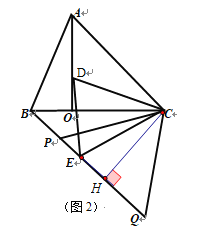
(2)过点C作CH⊥BQ于H,
∵△ABC是等腰三角形,∠ACB=45,AO是BC边上的高,
![]()
![]()
![]()
∴在![]() 中,
中, ![]()
![]()
![]()
![]()
![]()
![]() 时,
时, ![]() 取得最小值.
取得最小值.
最小值为: ![]()

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目