题目内容
【题目】如图,△ABC内接于⊙ O,其外角平分线AD交⊙ O于D,DM⊥ AC于M,下列结论中正确的是 ____________。
①DB=DC; ②AC+AB=2CM;③AC﹣AB=2AM; ④![]() .
.

【答案】①②③
【解析】试题解析:过点D作DF⊥BE于F,
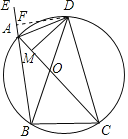
∵A、B、C、D四点共圆,
∴∠FAD=∠BCD,
∵外角平分线AD交⊙O于D,
∴∠FAD=∠DAC,
又∵∠DBC=∠DAC,
∴∠BCD=∠CBD,
∴①DB=DC,故此选项正确;
∵AD外角平分线,DF⊥BE,DM⊥AC于M,
∴DF=DM,
在△BFD≌△CMD中,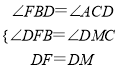
∴Rt△BFD≌Rt△CMD,
∴BF=CM,
又∵AF=AM,
∴②AC-AB=CM+AM-AB=CM+AM-CM+AF=CM+AM-CM+AM=2AM,故此选项正确;
∴③AC+AB=AM+MC+BF-FA=AM+MC+MC-AM=2CM,故此选项正确;
S△ABD和S△ABC的大小无法判断,④错误,

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】国家射击队将从甲、乙两名运动员中选拔一人参加奥运会比赛,对他们进行了六次测试,测试成绩如下表:(单位:环)
成绩 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加比赛更合适,请说明理由.


