题目内容
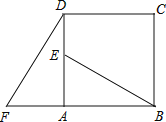
【题目】如图，贵阳市某中学数学活动小组在学习了“利用三角函数测高”后．选定测量小河对岸一幢建筑物BC的高度．他们先在斜坡上的D处，测得建筑物顶的仰角为30°．且D离地面的高度DE=5m．坡底EA=10m，然后在A处测得建筑物顶B的仰角是50°，点E，A，C在同一水平线上，求建筑物BC的高．（结果保留整数）
【答案】21m
【解析】试题分析：过点D作DH⊥BC于点M，得出四边形DECH是矩形，所以DH=EC，DE=HC，设BC的长度为xm，则BH=（x－5）m，由∠BDH=30°可以求出∠DBH=60°，进而表示出DH=
（x－5），然后表示出AC=
（x－5）－10，最后由BC= tan50°·AC列出方程，解出x即可.
试题解析：
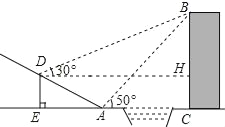
过点D作DH⊥BC于点M，
则四边形DHCE是矩形，DH=EC，DE=HC，
设BC的高度为xm，则BH=（x－5）m，
∵∠BDH=30°，
∴∠DBH=60°，
∴DH=BH·tan60°=
（x－5），
∴AC=EC－EA=
（x－5）－10，
∵∠BAC=50°，
∴BC= tan50°·AC，
∴x=tan50°·[
（x－5）]，
解得：x≈21，
答：建筑物BC的高约为21m．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】珠海市水务局对某小区居民生活用水情况进行了调査．随机抽取部分家庭进行统计，绘制成如下尚未完成的频数分布表和频率分布直方图．请根据图表，解答下列问题：
月均用水量（单位：吨 | 频数 | 频率 |
2≤x＜3 | 4 | 0.08 |
3≤x＜4 | a | b |
4≤x＜5 | 14 | 0.28 |
5≤x＜6 | 9 | c |
6≤x＜7 | 6 | 0.12 |
7≤x＜8 | 5 | 0.1 |
合计 | d | 1.00 |
（1）b= ，c= ，并补全频数分布直方图；
（2）为鼓励节约用水用水，现要确定一个用水量标准P（单位：吨），超过这个标准的部分按1.5倍的价格收费，若要使60%的家庭水费支出不受影响，则这个用水量标准P= 吨；
（3）根据该样本，请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户？
【题目】学完二次根式一章后，小易同学看到这样一题：“函数
中,自变量
的取值范围是什么？”这个问题很简单，根据二次根式的性质很容易得到自变量的取值范围.联想到一次函数，小易想进一步研究这个函数的图象和性质.以下是他的研究步骤：
第一步：函数中,自变量的取值范围是_____________.
第二步：根据自变量取值范围列表：
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
__________.
第三步：描点画出函数图象.
在描点的时候，遇到了
，
这样的点，小易同学用所学勾股定理的知识，找到了画图方法，如图所示：
你能否从中得到启发，在下面的
轴上标出表示
、
、
的点，并画出的函数图象.
第四步：分析函数的性质.
请写出你发现的函数的性质(至少写两条)：
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步：利用函数图象解含二次根式的方程和不等式.
（1）请在上面坐标系中画出
的图象，并估算方程
的解.
（2）不等式
的解是__________________.
