ÌâÄżÄÚÈĘ
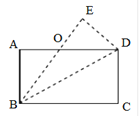
ĄŸÌâÄżĄżŁšÌâÎÄŁ©ŁšÌâÎÄŁ©ÔÚÊęѧĐËÈ€ĐĄŚé»î¶ŻÖĐŁŹĐĄÁÁœűĐĐÊęŃ§ÌœŸż»î¶ŻŁźĄśABCÊDZ߳€ÎȘ2”ĔȱßĐÎŁŹEÊÇACÉÏÒ»”㣏ХÁÁÒÔBEÎȘ±ßÏòBE”ÄÓÒČàŚś”ȱßÈęœÇĐÎBEFŁŹÁŹœÓCFŁź

Łš1Ł©ÈçÍŒ1ŁŹ”±”ăEÔÚÏ߶ÎACÉÏʱŁŹEFĄąBCÏàœ»ÓÚ”ăDŁŹĐĄÁÁ·ąÏÖÓĐÁœžöÈęœÇĐÎÈ«”ÈŁŹÇëÄăŐÒłöÀŽŁŹČąÖ€ĂśŁź
Łš2Ł©”±”ăEÔÚÏ߶ÎÉÏÔ˶ŻÊ±ŁŹ”ăFÒČËæŚĆÔ˶ŻŁŹÈôËıßĐÎABFC”ÄĂæ»ęÎȘ![]() ŁŹÇóAE”Äł€Łź
ŁŹÇóAE”Äł€Łź
Łš3Ł©ÈçÍŒ2ŁŹ”±”ăEÔÚAC”ÄŃÓł€ÏßÉÏÔ˶ŻÊ±ŁŹCFĄąBEÏàœ»ÓÚ”ăDŁŹÇëÄăÌœÇóĄśECD”ÄĂæ»ęS1Ó륜DBF”ÄĂæ»ęS2ÖźŒä”ÄÊęÁżčŰÏ”ŁźČąË”ĂśÀíÓÉŁź
Łš4Ł©ÈçÍŒ2ŁŹ”±ĄśECD”ÄĂæ»ęS1=![]() ʱŁŹÇóAE”Äł€Łź
ʱŁŹÇóAE”Äł€Łź
ĄŸŽđ°žĄżŁš1Ł©ĄśABEĄŐĄśCBFŁŹÖ€ĂśŒûœâÎöŁ»Łš2Ł©![]() Ł»Łš3Ł©S2©S1=
Ł»Łš3Ł©S2©S1=![]() ŁŹÖ€ĂśŒûœâÎöŁ»Łš4Ł©3
ŁŹÖ€ĂśŒûœâÎöŁ»Łš4Ł©3
ĄŸœâÎöĄżŁš1Ł©œáÂÛŁșĄśABEĄŐĄśCBFŁźÀíÓɔȱßÈęœÇĐΔÄĐÔÖÊŁŹžùŸĘSASŒŽżÉրÜŁ»
Łš2Ł©ÓÉĄśABEĄŐĄśCBFŁŹÍÆłöSĄśABE=SĄśBCFŁŹÍÆłöSËıßĐÎBECF=SĄśBEC+sĄśBCF=SĄśBCE+SĄśABE=SĄśABC=![]() ŁŹÓÉSËıßĐÎABCF=
ŁŹÓÉSËıßĐÎABCF=![]() ŁŹÍÆłöSĄśABE=
ŁŹÍÆłöSĄśABE=![]() ŁŹÔÙÀûÓĂÈęœÇĐΔÄĂæ»ęč«ÊœÇółöAEŒŽżÉŁ»
ŁŹÔÙÀûÓĂÈęœÇĐΔÄĂæ»ęč«ÊœÇółöAEŒŽżÉŁ»
Łš3Ł©œáÂÛŁșS2-S1=![]() ŁźÀûÓĂÈ«”ÈÈęœÇĐΔÄĐÔÖÊŒŽżÉրÜŁ»
ŁźÀûÓĂÈ«”ÈÈęœÇĐΔÄĐÔÖÊŒŽżÉրÜŁ»
Łš4Ł©ÊŚÏÈÇółöĄśBDF”ÄĂæ»ęŁŹÓÉCFĄÎABŁŹÔòĄśBDF”ÄBF±ßÉϔĞßÎȘ![]() ŁŹżÉ”ĂDF=
ŁŹżÉ”ĂDF=![]() ŁŹÉèCE=xŁŹÔò2+x=CD+DF=CD+
ŁŹÉèCE=xŁŹÔò2+x=CD+DF=CD+![]() ŁŹÍÆłöCD=x-
ŁŹÍÆłöCD=x-![]() ŁŹÓÉCDĄÎABŁŹżÉ”Ă
ŁŹÓÉCDĄÎABŁŹżÉ”Ă![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹÇółöxŒŽżÉŁ»
ŁŹÇółöxŒŽżÉŁ»
Łš1Ł©œáÂÛŁșĄśABEĄŐĄśCBFŁź
ÀíÓÉŁșÈçÍŒ1ÖĐŁŹ

ĄßĄśABCŁŹĄśBEF¶ŒÊǔȱßÈęœÇĐÎŁŹ
ĄàBA=BCŁŹBE=BFŁŹĄÏABC=ĄÏEBFŁŹ
ĄàĄÏABE=ĄÏCBFŁŹ
ĄàĄśABEĄŐĄśCBFŁź
Łš2Ł©ÈçÍŒ1ÖĐŁŹĄßĄśABEĄŐĄśCBFŁŹ
ĄàSĄśABE=SĄśBCFŁŹ
ĄàSËıßĐÎBECF=SĄśBEC+sĄśBCF=SĄśBCE+SĄśABE=SĄśABC=![]() ŁŹ
ŁŹ
ĄßSËıßĐÎABCF=![]() ŁŹ
ŁŹ
ĄàSĄśABE=![]() ŁŹ
ŁŹ
Ąà![]() AEABsiin60Ąă=
AEABsiin60Ąă=![]() ŁŹ
ŁŹ
ĄàAE=![]() Łź
Łź
Łš3Ł©œáÂÛŁșS2-S1=![]() Łź
Łź
ÀíÓÉŁșÈçÍŒ2ÖĐŁŹ

ĄßĄśABCŁŹĄśBEF¶ŒÊǔȱßÈęœÇĐÎŁŹ
ĄàBA=BCŁŹBE=BFŁŹĄÏABC=ĄÏEBFŁŹ
ĄàĄÏABE=ĄÏCBFŁŹ
ĄàĄśABEĄŐĄśCBFŁŹ
ĄàSĄśABE=SĄśBCFŁŹ
ĄßSĄśBCF-SĄśBCE=S2-S1ŁŹ
ĄàS2-S1=SĄśABE-SĄśBCE=SĄśABC=![]() Łź
Łź
Łš4Ł©ÓÉŁš3Ł©żÉÖȘŁșSĄśBDF-SĄśECD=![]() ŁŹ
ŁŹ
ĄßSĄśECD=![]() ŁŹ
ŁŹ
ĄàSĄśBDF=![]() ŁŹ
ŁŹ
ĄßĄśABEĄŐĄśCBFŁŹ
ĄàAE=CFŁŹĄÏBAE=ĄÏBCF=60ĄăŁŹ
ĄàĄÏABC=ĄÏDCBŁŹ
ĄàCFĄÎABŁŹÔòĄśBDF”ÄBF±ßÉϔĞßÎȘ![]() ŁŹżÉ”ĂDF=
ŁŹżÉ”ĂDF=![]() ŁŹ
ŁŹ
ÉèCE=xŁŹÔò2+x=CD+DF=CD+![]() ŁŹ
ŁŹ
ĄàCD=x-![]() ŁŹ
ŁŹ
ĄßCDĄÎABŁŹ
Ąà![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹ
ŁŹ
»ŻŒò”ĂŁș3x2-x-2=0ŁŹ
œâ”Ăx=1»ò![]() ŁšÉáÆúŁ©ŁŹ
ŁšÉáÆúŁ©ŁŹ
ĄàCE=1ŁŹAE=3Łź