题目内容
【题目】一幢楼的楼顶端挂着一幅长10米的宣传条幅AB，某数学兴趣小组在一次活动中，准备测量该楼的高度，但被建筑物FGHM挡住，不能直接到达楼的底部，他们在点D处测得条幅顶端A的仰角∠CDA＝45°，向后退8米到E点，测得条幅底端B的仰角∠CEB＝30°（点C，D，E在同一直线上，EC⊥AC）．请你根据以上数据，帮助该兴趣小组计算楼高AC（结果精确到0.01米，参考数据：
≈1.732，
≈1.414）．
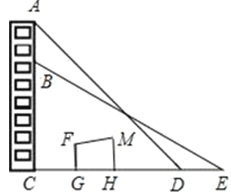
【答案】34.59米
【解析】
设AC＝x米，根据等腰三角形的性质用x表示出CD，根据正切的定义列式计算，得到答案．
解：设AC＝x米，则BC＝（x﹣10）米，
在Rt△ACD中，∠CDA＝∠CAD＝45°，
所以CD＝AC＝x，
在Rt△ECB中，CE＝CD+DE＝x+8．
所以tan∠CEB＝
，即
＝tan30°＝
．
解得，x＝
≈34.59．
答：楼高AC约为34.59米．
练习册系列答案
相关题目
