��Ŀ����
����Ŀ��Ϊ�˺��ᆪ�����㴫ͳ�Ļ���ij��ѧ�ٰ��˾����Ļ�֪ʶ������������ǣ�ÿλ����ѡ�ֻش�100��ѡ���⣬���һ���1�֣��������÷֡����۷֣������ȫ�����ѡ�ֵĴ���������������ͳ�ƣ����������Ƴ�����ͼ����
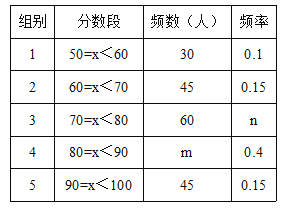
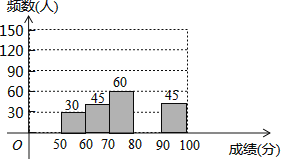
�������ͼ����Ϣ������������⣺
��1������m=������n=������
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��ȫ�����ѡ�ֳɼ�����λ�����ڵڼ��飻
��4�����÷���80�����ϣ���80�֣���ѡ�ֿɻ����ߴ����в���ѡ��������ɷ�1�ˣ�������ѡ��ǡ���ǻ��ߵĸ��ʣ�
���𰸡���1��m=120��n=0.2����2���𰸼���������3����һ�飻��4��0.55
�������������������1�����ݱ���������ȫ�����ѡ�ֵ��������Ӷ��������m��ֵ��n��ֵ����1�����ݣ�1���е�m��ֵ�����Խ���ȫƵ���ֲ�ֱ��ͼ����3�����ݱ���������ȫ�����ѡ�ֳɼ�����λ�����ڵڼ��飻��4�����ݱ����е����ݿ����������ѡ��ǡ���ǻ��ߵĸ��ʣ�
�����������1���ɱ���ɵã�ȫ�������ѡ�������У�30��0.1=300��
��m=300��0.4=120��n=60��300=0.2��
��2����ȫ��Ƶ���ֲ�ֱ��ͼ��ͼ��ʾ��
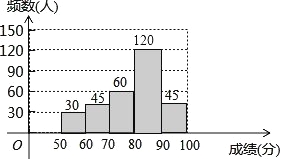
��3����35+45=75��75+60=135��135+120=255�� ��ȫ�����ѡ�ֳɼ�����λ������80��x��90��һ�飻
��4��������ɵã�![]() �� ������ѡ��ǡ���ǻ��ߵĸ�����0.55��
�� ������ѡ��ǡ���ǻ��ߵĸ�����0.55��