题目内容
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 和
和![]() 交于点
交于点![]() .
.
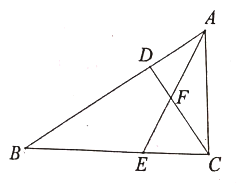
(1)若![]() ,则
,则![]() ____________
____________![]() ,
,![]() ____________
____________![]() ;
;
(2)结合(1)中的结果,探究![]() 和
和![]() 的关系,并说明理由.
的关系,并说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,见解析.
,见解析.
【解析】
(1)根据∠ACD+∠BAC=∠B+∠BAC=90°,可得∠ACD=∠B,再根据AE是角平分线,可得∠BAE=∠CAF,再根据∠CFE是△ACF的外角,∠CEF是△ABE的外角,即可得到∠CFE和∠CEF的度数;
(2)根据∠ACD+∠BAC=∠B+∠BAC=90°,可得∠ACD=∠B,再根据AE是角平分线,可得∠BAE=∠CAF,再根据∠CFE是△ACF的外角,∠CEF是△ABE的外角,即可得到∠CFE=CAF+∠ACD,∠CEF=∠B+∠BAE,进而得出∠CFE=∠CEF.
(1)∵∠ACB=90°,CD是高,∠B=40°,
∴∠ACD+∠BAC=∠B+∠BAC=90°,
∴∠ACD=∠B=40°,∠BAC=50°,
又∵AE是角平分线,
∴∠BAE=∠CAF=25°,
∵∠CFE是△ACF的外角,∠CEF是△ABE的外角,
∴∠CFE=∠CAF+∠ACD=65°,∠CEF=∠B+∠BAE=65°,
故答案为:65;65;
(2)∠CFE和∠CEF相等,
理由:∵∠ACB=90°,CD是高,
∴∠ACD+∠BAC=∠B+∠BAC=90°,
∴∠ACD=∠B,
又∵AE是角平分线,
∴∠BAE=∠CAF,
∵∠CFE是△ACF的外角,∠CEF是△ABE的外角,
∴∠CFE=CAF+∠ACD,∠CEF=∠B+∠BAE,
∴∠CFE=∠CEF.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元