题目内容
【题目】已知:在△ABC中,∠B=∠C,D,E分别是线段BC,AC上的一点,且AD=AE,
(1)如图1,若∠BAC=90°,D是BC中点,则∠2的度数为_____;
(2)借助图2探究并直接写出∠1和∠2的数量关系_____.
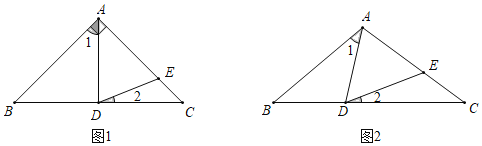
【答案】22.5 ∠1=2∠2
【解析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠CDE.
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠CDE.
解:(1)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵∠B=∠C,∠BAC=90°,D是BC中点,
∴∠BAD=45°,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,
∴∠2=22.5°;
(2)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,∠1=2∠2.

【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.