题目内容
如图(1),矩形纸片ABCD,把它沿对角线BD向上折叠,
(1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图痕迹,不写作法)
(2)折叠后重合部分是什么图形?说明理由.
(1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图痕迹,不写作法)
(2)折叠后重合部分是什么图形?说明理由.

(1) (2)等腰三角形,理由见解析
(2)等腰三角形,理由见解析
 (2)等腰三角形,理由见解析
(2)等腰三角形,理由见解析解:(1)作图如下:

(2)等腰三角形。理由如下:
∵△BDE是△BDC沿BD折叠而成,∴△BDE≌△BDC。∴∠FDB=∠CDB。om]
∵四边形ABCD是矩形,∴AB∥CD。∴∠ABD=∠BDC。∴∠FDB=∠BDC。
∴△BDF是等腰三角形。
(1)根据折叠的性质,可以作∠BDF=∠BDC,∠EBD=∠CBD,则可求得折叠后的图形。
作法如下:
作∠BDG=∠BDC,在射线DG上截取DE=DC,连接BE;
作∠DBH=∠DBC,在射线BH上截取BE=BC,连接DE;
作∠BDG=∠BDC,过B点作BH⊥DG,垂足为E;
作∠DBH=∠DBC,过,D点作DG⊥BH,垂足为E;
分别以D、B为圆心,DC、BC的长为半径画弧,两弧交于点E,连接DE、BE。
则△DEB为所求做的图形。
(2)由折叠的性质,易得∠FDB=∠CDB,又由四边形ABCD是矩形,可得AB∥CD,即可证得∠FDB=∠FBD,即可证得△FBD是等腰三角形。

(2)等腰三角形。理由如下:
∵△BDE是△BDC沿BD折叠而成,∴△BDE≌△BDC。∴∠FDB=∠CDB。om]
∵四边形ABCD是矩形,∴AB∥CD。∴∠ABD=∠BDC。∴∠FDB=∠BDC。
∴△BDF是等腰三角形。
(1)根据折叠的性质,可以作∠BDF=∠BDC,∠EBD=∠CBD,则可求得折叠后的图形。
作法如下:
作∠BDG=∠BDC,在射线DG上截取DE=DC,连接BE;
作∠DBH=∠DBC,在射线BH上截取BE=BC,连接DE;
作∠BDG=∠BDC,过B点作BH⊥DG,垂足为E;
作∠DBH=∠DBC,过,D点作DG⊥BH,垂足为E;
分别以D、B为圆心,DC、BC的长为半径画弧,两弧交于点E,连接DE、BE。
则△DEB为所求做的图形。
(2)由折叠的性质,易得∠FDB=∠CDB,又由四边形ABCD是矩形,可得AB∥CD,即可证得∠FDB=∠FBD,即可证得△FBD是等腰三角形。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
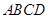 中,
中,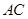 是对角线.点
是对角线.点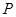 为矩形外一点且满足
为矩形外一点且满足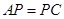 ,
,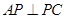 .
.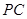 交
交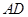 于点
于点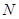 ,连接
,连接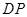 ,过点
,过点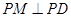 交
交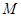 .
.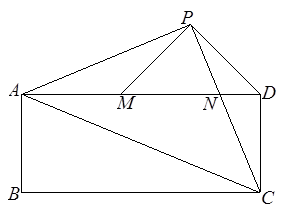
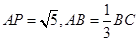 ,求矩形
,求矩形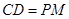 ,求证:
,求证: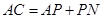 .
.
 ACF与
ACF与
 中,
中, ∥
∥ ,
, ,
, ,
, ,
, ,将
,将 平移到
平移到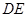 处。
处。
 是直角三角形吗?请说明理由;
是直角三角形吗?请说明理由; 上的高;
上的高;
