题目内容
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
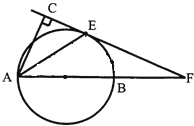
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

【答案】(1)![]() ;(2)①
;(2)①![]() ,②6.
,②6.
【解析】
试题分析:(1)根据辅助线的作法可得△AEF≌△CEB,△AFP∽△DBP,然后利用它们的性质可得![]() =
=![]() ;(2)①过点A作AF∥DB,交BE的延长线于点F,可得△AEF≌△CEB,△AFP∽△DBP,然后利用它们的性质可得
;(2)①过点A作AF∥DB,交BE的延长线于点F,可得△AEF≌△CEB,△AFP∽△DBP,然后利用它们的性质可得![]() =
=![]() ;②根据条件DC:BC:AC=1:2:3 ,CD=2,得出BC, AC,CE,AE的长,由勾股定理可得 EF的长,再利用△AFP∽△DBP的性质可求出BP的长.
;②根据条件DC:BC:AC=1:2:3 ,CD=2,得出BC, AC,CE,AE的长,由勾股定理可得 EF的长,再利用△AFP∽△DBP的性质可求出BP的长.
试题解析:(1)![]() 的值为
的值为![]() .
.
(2)①过点A作AF∥DB,交BE的延长线于点F,

∵DC︰BC=1︰2,
∴BC=2k.
∴DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
又∵∠2=∠3,
∴△AEF≌△CEB.
∴AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP.
∴![]() .
.
∴![]() =
=![]() .
.
②∵DC:BC:AC=1:2:3 ,CD=2,∴BC=4 AC=6
∴ CE=AE=![]() AC =3
AC =3
∴ 由勾股定理可得: EF=5,∴BF=10
∵ ![]() =
=![]() ,△AFP∽△DBP,
,△AFP∽△DBP,
∴![]()
∴BP=6

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目